题目内容
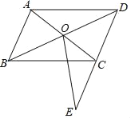
【题目】如图,在ABCD中,对角线AC、BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,已知AB=6,BC=8,CE=2
(1)求CF的长.
(2)设△COF的面积为S1,△COD的面积为S2,直接写出S1:S2的值.
【答案】(1)CF=![]() .(2)S1:S2=1:5.
.(2)S1:S2=1:5.
【解析】
(1)首先过点O作OM//AB, 交BC于点M, 易得ΔCFE∽ΔEMO,, 然后由相似三角形的对应边成比例, 求得答案;
(2) 易得CF:BF=1:4,由三角形相似△OBF的面积为4m,可得S1:S2的值.
解:过O作OM∥BC交CD于M,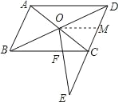
∵在ABCD中,BO=DO,CD=AB=4,AD=BC=6,
∴CM=![]() CD=3,OM=
CD=3,OM=![]() BC=4,
BC=4,
∵OM∥CF,
∴△CFE∽△EMO,
∴![]() ,
,
即![]() ,
,
∴CF=![]() .
.
(2)设S1=m,
∵CF:BF=1:4,
∴![]() 的面积为4m,
的面积为4m,
![]() 的面积=
的面积=![]() 的面积=5m,
的面积=5m,
∴S1:S2=1:5.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?