题目内容
【题目】图①是一个长为![]() 、宽为
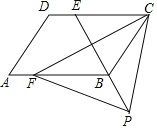
、宽为![]() 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
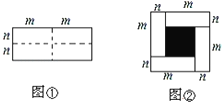
(1)请用两种不同的方法求图②中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图②请你写出下列三个代数式:![]() 之间的等量关系.
之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,求
,求![]() 的值;
的值;
②已知:![]() ,求:
,求:![]() 的值.
的值.
【答案】(1)方法1:(m-n)2;方法2:(m+n)2-4mn;(2)(m-n)2=(m+n)2-4mn;(3)①1;②±3.
【解析】
(1)大正方形的面积减去矩形的面积即可得出阴影部分(小正方形)的面积;
(2)由面积关系容易得出结论;
(3)①根据(2)所得出的关系式,容易求出结果;
②先求出![]() ,再求(a
,再求(a![]() )2,即可得出结果.
)2,即可得出结果.
(1)方法1:(m+n)2﹣4mn,方法2:(m﹣n)2.
故答案为:(m+n)2﹣4mn,(m﹣n)2;
(2)(m﹣n)2=(m+n)2﹣4mn;
(3)①(a+b)2=(a﹣b)2+4ab=52+4×(﹣6)=1;
②∵![]() ,
,
∴![]() ,
,
∴(a![]() )2=(a
)2=(a![]() )2+4×a
)2+4×a![]() 12+8=9,
12+8=9,
∴a![]() ±3.
±3.

【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数。
(2)若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额,你认为这个定额是否合理,为什么?
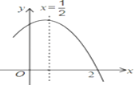
【题目】二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
下列说法正确的是( )
A. 抛物线的开口向下
B. 当x>﹣![]() 时,y随x的增大而增大
时,y随x的增大而增大
C. 二次函数的最小值是﹣2
D. 抛物线的对称轴是x=1