题目内容
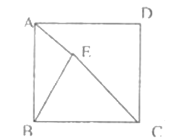
【题目】如图,点![]() 为正方形
为正方形![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,则
,则![]() _________.
_________.
【答案】![]()
【解析】
作EG⊥AB于G,EH⊥BC于H,由四边形ABCD是正方形,得到∠ABC=90°,由四边形BHEG是矩形,得到EG=BH,BG=EH,在Rt△ABE中根据勾股定理可求出AB的长,根据三角形的面积公式得到EG的长,在Rt△BGE中根据勾股定理得到BG的值,再在Rt△CEH中根据勾股定理得到CE的值即可.
作EG⊥AB于G,EH⊥BC于H,
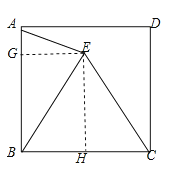
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴四边形BHEG是矩形,∴
EG=BH,BG=EH,
∵∠AEB=90°,若AE=2,BE=3,
∴AB=![]() ,
,
∵S△ABE=![]() ABEG=
ABEG=![]() AEBE,
AEBE,
∴![]() EG=2×3,
EG=2×3,
∴EG=![]() ,
,
∴BG=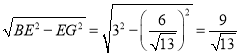 ,
,
∴HE=BG=![]() ,BH=EG=
,BH=EG=![]() ,
,
∴CH=BC-BH=![]() ,
,
∴CE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目