��Ŀ����
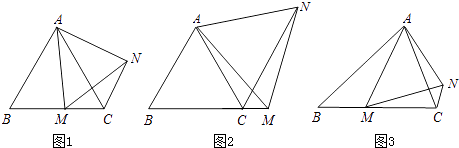
����Ŀ����ͼ����ABC�ǵȱ������Σ���D��BC����һ���㣬��E��F�ֱ���AB��AC���ϣ�����AD��DE��DF���ҡ�ADE=��ADF=60�㣮
С��ͨ���۲졢ʵ�飬������룺�ڵ�D�˶��Ĺ����У�ʼ����AE=AF��С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1������AD�ǡ�EDF�Ľ�ƽ���ߣ������ADF��ȫ�������Σ�Ȼ��ͨ�����������ε����֪ʶ��֤��
�뷨2������AD�ǡ�EDF�Ľ�ƽ���ߣ������ƽ���ߵ����ʶ����Ļ���ͼ�Σ�Ȼ��ͨ��ȫ�������ε����֪ʶ��֤��
�뷨3������ACD�Ƶ�A˳ʱ����ת����ABG��ʹ��AC��AB�غϣ�Ȼ��ͨ��ȫ�������ε����֪ʶ��֤��
����ο�������뷨������С��֤��AE=AF����һ�ַ������ɣ�

���𰸡�������
��������
�뷨1����DE�Ͻ�ȡDG=DF������AG�����ж���ADG�ա�ADF���õ�AG=AF���ٸ��ݡ�AEG=��AGE���ó�AE=AG�������õ�AE=AF��
�뷨2����A��AG��DE��G��AH��DF��H�����ݽ�ƽ���ߵ����ʵõ�AG=AH�������ж���AEG�ա�AFH�����ɵõ�AE=AF��
�뷨3������ACD���ŵ�A˳ʱ����ת����ABG��ʹ��AC��AB�غϣ�����DG���ж���AGD�ǵȱ������Σ������ó���AGE�ա�ADF�����ɵõ�AE=AF��
֤����
�뷨1����ͼ����DE�Ͻ�ȡDG=DF������AG��
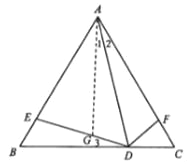
�ߡ�ABC�ǵȱ������Σ�
���B=��C=60�㣬
�ߡ�ADE=��ADF=60�㣬AD=AD��
���ADG�ա�ADF��
��AG=AF����1=��2��
�ߡ�ADB=60��+��3=60��+��2��
���3=��2��
���3=��1��
�ߡ�AEG=60��+��3����AGE=60��+��1��
���AEG=��AGE��
��AE=AG��
��AE=AF��
�뷨2����ͼ����A��AG��DE��G��AH��DF��H��
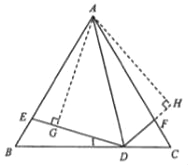
�ߡ�ADE=��ADF=60�㣬
��AG=AH��
�ߡ�FDC=60�㩁��1��
���AFH=��DFC=60��+��1��
�ߡ�AED=60��+��1��
���AEG=��AFH��
���AEG�ա�AFH��
��AE=AF��
�뷨3����ͼ������ACD���ŵ�A˳ʱ����ת����ABG��ʹ��AC��AB�غϣ�����DG��

���ABG�ա�ACD��
��AG=AD����GAB=��DAC��
�ߡ�ABC�ǵȱ������Σ�
���BAC=��ABC=��C=60�㣬
���GAD=60�㣬
���AGD�ǵȱ������Σ�
���ADG=��AGD=60�㣬
�ߡ�ADE=60�㣬
��G��E��D���㹲�ߣ�
���AGE�ա�ADF��
��AE=AF��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�