题目内容
【题目】如图,已知点D在△ABC的边AB上,且AD=CD,

(1)用直尺和圆规作∠BDC的平分线DE,交BC于点E(不写作法,保留作图痕迹);
(2)在(1)的条件下,判断DE与AC的位置关系,并写出证明过程.
【答案】(1)见解析;(2)DE∥AC,理由见解析
【解析】
(1)根据角平分线的尺规作图可得;
(2)先由AD=CD知∠A=∠DCA,继而得∠BDC=∠A+∠DCA=2∠A,再由DE平分∠BDC知∠BDC=2∠BDE,从而得∠BDE=∠A,从而得证.
解:(1)如图所示,DE即为所求.
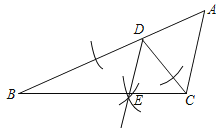
(2)DE∥AC.
理由如下:
因为AD=CD,
所以∠A=∠DCA,
所以∠BDC=∠A+∠DCA=2∠A,
因为DE平分∠BDC,
所以∠BDC=2∠BDE,
所以∠BDE=∠A,
所以DE∥AC.

练习册系列答案
相关题目