题目内容
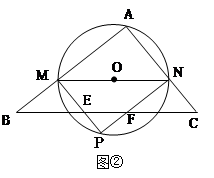
如图:等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.

(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2DO2;
(3)在(2)的条件下,若 ,求
,求 的值.
的值.

(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2DO2;
(3)在(2)的条件下,若
 ,求
,求 的值.
的值.(1)根据等圆的性质可得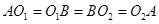 ,即可证得结论;(2)根据菱形的性质可得∠
,即可证得结论;(2)根据菱形的性质可得∠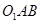 =∠
=∠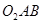 ,根据CE是⊙O1的切线,AC是⊙O1的直径可得∠
,根据CE是⊙O1的切线,AC是⊙O1的直径可得∠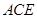 =∠
=∠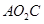 =90°,即可证得△ACE∽△AO2D,根据相似三角形的性质求解即可;(3)
=90°,即可证得△ACE∽△AO2D,根据相似三角形的性质求解即可;(3)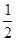
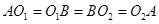 ,即可证得结论;(2)根据菱形的性质可得∠
,即可证得结论;(2)根据菱形的性质可得∠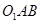 =∠
=∠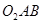 ,根据CE是⊙O1的切线,AC是⊙O1的直径可得∠
,根据CE是⊙O1的切线,AC是⊙O1的直径可得∠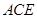 =∠
=∠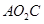 =90°,即可证得△ACE∽△AO2D,根据相似三角形的性质求解即可;(3)
=90°,即可证得△ACE∽△AO2D,根据相似三角形的性质求解即可;(3)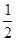
试题分析:(1)根据等圆的性质可得
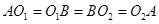 ,即可证得结论;
,即可证得结论;(2)根据菱形的性质可得∠
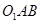 =∠
=∠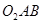 ,根据CE是⊙O1的切线,AC是⊙O1的直径可得∠
,根据CE是⊙O1的切线,AC是⊙O1的直径可得∠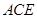 =∠
=∠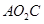 =90°,即可证得△ACE∽△AO2D,根据相似三角形的性质求解即可;
=90°,即可证得△ACE∽△AO2D,根据相似三角形的性质求解即可;(3)根据菱形的性质可得
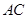 ∥
∥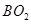 ,即可证得△ACD∽△
,即可证得△ACD∽△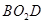 ,再根据相似三角形的性质及
,再根据相似三角形的性质及 求解即可.
求解即可.(1)∵⊙O1与⊙O2是等圆,
∴
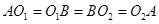
∴四边形
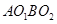 是菱形;
是菱形;(2)∵四边形
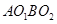 是菱形
是菱形 ∴∠
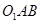 =∠
=∠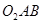
∵CE是⊙O1的切线,AC是⊙O1的直径
∴∠
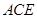 =∠
=∠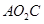 =90°
=90°∴△ACE∽△AO2D
∴
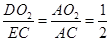 ,即
,即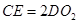 ;
;(3)∵四边形
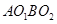 是菱形
是菱形∴
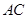 ∥
∥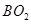
∴△ACD∽△
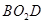
∴
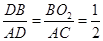
∴
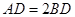
∵
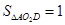
∴
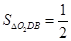 .
. 点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
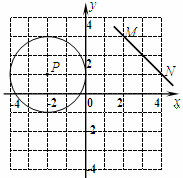
 轴上截得的线段长度;
轴上截得的线段长度;


 和7
和7
 为⊙O的半径,点C在⊙O上,且∠ACB=36°,则∠OAB= 度。
为⊙O的半径,点C在⊙O上,且∠ACB=36°,则∠OAB= 度。
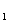 和⊙O
和⊙O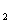 相切,两圆的圆心距为9cm,⊙
相切,两圆的圆心距为9cm,⊙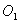 的半径为4cm,则⊙O
的半径为4cm,则⊙O