Question

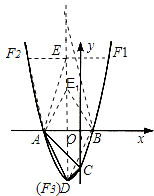
【题目】如图，抛物线y=x2+bx+c的顶点为D（﹣1，﹣4），与y轴交于点C（0，﹣3），与x轴交于A，B两点（点A在点B的左侧）．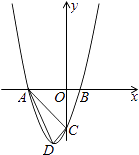

（1）求抛物线的解析式；
（2）连接AC，CD，AD，试证明△ACD为直角三角形；
（3）若点E在抛物线的对称轴上，抛物线上是否存在点F，使以A，B，E，F为顶点的四边形为平行四边形？若存在，求出所有满足条件的点F的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：由题意得 ，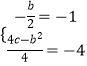

解得：b=2，c=﹣3，

则解析式为：y=x2+2x﹣3

（2）

解：由题意结合图形

则解析式为：y=x2+2x﹣3，

解得x=1或x=﹣3，

由题意点A（﹣3，0），

∴AC= ，CD= ，AD= ，

由AC2+CD2=AD2，

所以△ACD为直角三角形

（3）

解：∵A（﹣3，0），B（1，0），

∴AB=4，

∵点E在抛物线的对称轴上，

∴点E的横坐标为﹣1，

当AB为平行四边形的一边时，EF=AB=4，

∴F的横坐标为3或﹣5，

把x=3或﹣5分别代入y=x2+2x﹣3，得到F的坐标为（3，12）或（﹣5，12）；

当AB为平行四边形的对角线时，由平行四边形的对角线互相平分，

∴F点必在对称轴上，即F点与D点重合，

∴F（﹣1，﹣4）．

∴所有满足条件的点F的坐标为（3，12），（﹣5，12），（﹣1，﹣4）．

【解析】（1）由定点列式计算，从而得到b，c的值而得解析式；（2）由解析式求解得到点A，得到AC，CD，AD的长度，而求证；（3）由（2）得到的结论，进行代入，要使以A，B，E，F为顶点的四边形是平行四边形，必须满足的条件是AB平行且等于EF，那么只需将E点的坐标向左或向右平移AB长个单位即可得出F点的坐标，然后将得出的F点坐标代入抛物线的解析式中，即可判断出是否存在符合条件的F点．
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点．