题目内容
【题目】如图，在△ABC中，D、E分别是边AB、AC的中点，O是三角形内部一点，连接OB、OC，G、H分别是OC、OB的中点，试说明四边形DEGH是平行四边形．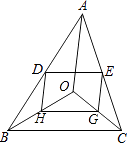 
【答案】解：在△ABC中，∵D、E分别是边AB、AC的中点，
∴DE 
BC，
同理，在△OBC中，HG BC，
所以，DE HG，
所以，四边形DEGH是平行四边形
【解析】根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC且DE= 
BC，GH∥BC且GH= BC，从而得到DE∥GH，DE=GH，再利用一组对边平行且相等的四边形是平行四边形证明即可．
【考点精析】本题主要考查了三角形中位线定理和平行四边形的判定的相关知识点，需要掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形才能正确解答此题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
