Question

【题目】如图，△ABC的内心在y轴上，点C的坐标为（2，0），点B的坐标是（0，2），直线AC的解析式为 ，则tanA的值是 ．

Answer 1

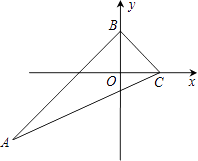
【答案】
【解析】解：根据三角形内心的特点知∠ABO=∠CBO，
∵已知点C、点B的坐标，
∴OB=OC，∠OBC=45°，∠ABC=90°可知△ABC为直角三角形，BC=2 ，
∵点A在直线AC上，设A点坐标为（x， x﹣1），
根据两点距离公式可得：
AB2=x2+ ，
AC2=（x﹣2）2+ ，
在Rt△ABC中，
AB2+BC2=AC2 ，
解得：x=﹣6，y=﹣4，
∴AB=6 ，
∴tanA= = = ．
所以答案是： ．
【考点精析】本题主要考查了一次函数的性质的相关知识点，需要掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小才能正确解答此题．