��Ŀ����
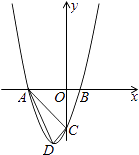
����Ŀ����ͼ�����мס�������С�ֶӷֱ�ͬʱ��B��C���س���ǰ��A�أ�������·BA�н���������·CA�н�����֪C��A����ƫ��55�㷽��AB���¶�Ϊ1��5��ͬʱ���ڵ���ԭ�����BC·����ʯ��������BC·����λ��A�����Ϸ�������һ���ϴ�H����������BC·�Σ���֪BHΪ12000m��
��1����BC�ij��ȣ�
��2����������ֶ���ǰ��A��ʱ����ǰ�У��Ҽ��ٶ����ҵ��ٶȵ����������ж��ĸ��ֶ��ȵ���A�أ���tan55���1.4��sin55���0.84��cos55���0.6�� ![]() ��5.01���������������
��5.01���������������
���𰸡�
��1��
�⣺����AH
��H��A�����Ϸ���
��AH��BC��
��AB���¶�Ϊ��1��5��
����Rt��ABH�� ![]() =
= ![]() ��
��
��AH=12000�� ![]() =2400��m��
=2400��m��
����Rt��ACH��tan��HAC= ![]() ��
��
��1.4= ![]() ����CH=3360m
����CH=3360m
��BC=BH+CH=15360m��
��2��
�⣺���ȵ���Ŀ�ĵأ��������£���Rt��ACH�У�cos��HAC= ![]() ����0.6=
����0.6= ![]() ����AC=
����AC= ![]() =4000��m����
=4000��m����
��Rt��ABH�� ![]() =
= ![]() ����AH=x��BH=5x��
����AH=x��BH=5x��
�ɹ��ɶ����ã�AB= ![]() =
= ![]() x��5.01��2400=12024��m����
x��5.01��2400=12024��m����
��3AC=12000��12024=AB�� ���ҷֶ��ȵ���Ŀ�ĵأ�
��������(1)�������¶ȵĶ���ó�AH�ij���������tan��HAC= ![]() ���ó�CH�ij��������ó��𰸣�(2)�����ù��ɶ����ó�AB�ij�����cos��HAC=
���ó�CH�ij��������ó��𰸣�(2)�����ù��ɶ����ó�AB�ij�����cos��HAC= ![]() ���ó�AC�ij������ó��𰸣�
���ó�AC�ij������ó��𰸣�

 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�