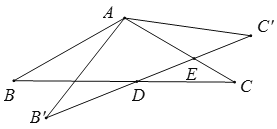
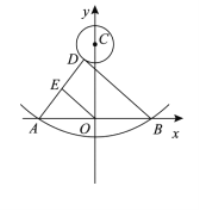
题目内容
【题目】点C为线段
上一点，以
为斜边作等腰
，连接
，在
外侧，以为斜边作等腰
，连接
．
（1）如图1，当
时：
①求证：
；
②判断线段与
的数量关系，并证明；
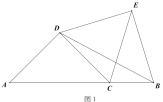
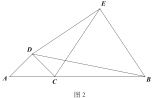
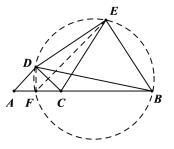
（2）如图2，当
时，与的数量关系是否保持不变？
对于以上问题，小牧同学通过观察、实验，形成了解决该问题的几种思路：
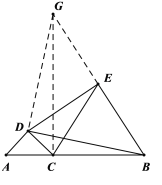
想法1：尝试将点D为旋转中心，过点D作线段垂线，交
延长线于点G，连接
；通过证明
解决以上问题；
想法2：尝试将点D为旋转中心，过点D作线段垂线，垂足为点G，连接
．通过证明
解决以上问题；
想法3：尝试利用四点共圆，过点D作垂线段
，连接
，通过证明D、F、B、E四点共圆，利用圆的相关知识解决以上问题．
请你参考上面的想法，证明
（一种方法即可）．
【答案】（1）①证明见解析；②
，证明见解析；（2）证明见解析．
【解析】
（1）①如图（见解析），先根据直角三角形的性质得出
，再根据等腰三角形的三线合一得出
是斜边AC上的中线，然后根据直角三角形的性质
，最后根据等量代换即可得证；
②先结合①的结论、等腰直角三角形的性质
，
，
，再根据角的和差、直角三角形的性质得出
，然后根据等边三角形的判定与性质得出
，由此即可证出；
（2）想法1：先根据等腰三角形的性质、角的和差得出
，再根据等腰三角形的性质可得
，然后根据三角形全等的判定定理与性质可得
，从而可得
，最后根据直角三角形斜边上的中线等于斜边的一半即可得证；
想法2：先根据等腰直角三角形的性质、角的和差得出
，
，再根据相似三角形的判定与性质得出
，从而可得
平分
，然后根据等腰三角形的三线合一可得是
的垂直平分线，最后根据垂直平分线的性质、等量代换即可得证；
想法3：先根据垂直的定义、等腰直角三角形的定义得出
，
，从而可得
，由此可证出D、F、B、E四点共圆，再根据圆周角定理可得
，然后同想法2的方法即可得证．
（1）①过点D作
于F
是等腰三角形
是斜边AC上的中线（等腰三角形的三线合一）
；
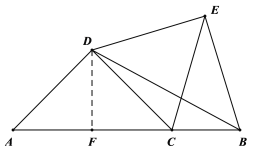
②，证明如下：
等腰与等腰
中
，，
是等边三角形
；
（2）想法1：如图，过点D作线段
垂线，交
延长线于点G，连接
是等腰直角三角形
，
，
，即
是等腰直角三角形
，即
在
和
中，
是直角三角形
点E是BG的中点，即CE是斜边BG上的中线
；
想法2：如图，过点D作线段
垂线，垂足为点G，连接
是等腰直角三角形
，
，
，
是等腰直角三角形
，即
是等腰直角三角形
，
，
，即
在和
中，
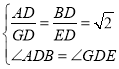
平分
是等腰直角三角形
是的垂直平分线（等腰三角形的三线合一）
即；
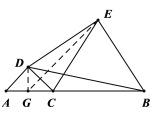
想法3：如图，过点D作垂线段，连接
是等腰直角三角形
，，
D、F、B、E四点共圆
同想法2可证：
是的垂直平分线
即．
