题目内容
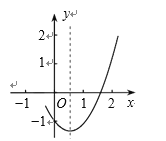
【题目】如图抛物线经![]() 过点
过点![]() ,tan∠CAB=3,且
,tan∠CAB=3,且![]() .
.
(1)求抛物线的解析式及其对称轴;
(2)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为
的面积分为![]() 两部分,求点
两部分,求点![]() 的坐标.
的坐标.
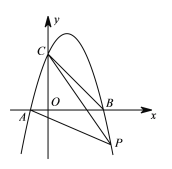
【答案】(1)y=-x2+2x+3;对称轴为:x=1;(2)点P的坐标为(4,-5)或(8,-45).
【解析】
(1)OB=OC,则点B(3,0),则抛物线的表达式为:y=a(x+1)(x-3)=a(x2-2x-3)=ax2-2ax-3a,C点坐标代入可求出a的值,得到抛物线方程,再进行配方即可求出对称轴方程;
(2)根据S△PCB:S△PCA=![]() EB×(yC-yP):
EB×(yC-yP):![]() AE×(yC-yP)=BE:AE求出点E坐标,进而可求出直线PC的解析式,再与抛物线方程联立方程组,求解方程组即可求得点P坐标.
AE×(yC-yP)=BE:AE求出点E坐标,进而可求出直线PC的解析式,再与抛物线方程联立方程组,求解方程组即可求得点P坐标.
(1)∵![]()
∴OA=1,
∵tan∠CAB= ![]() 3
3
∴OC=3
∵OB=OC,
∴点B(3,0),C(0,3)
则抛物线的表达式为:y=a(x+1)(x-3)=a(x2-2x-3)=ax2-2ax-3a,
故-3a=3,解得:a=-1,
故抛物线的表达式为:y=-x2+2x+3=-(x-1)2+4,
函数的对称轴为:x=1;
(2)如图,设直线CP交x轴于点E,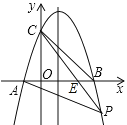
直线CP把四边形CBPA的面积分为3:5两部分,
又∵S△PCB:S△PCA=![]() EB×(yC-yP):
EB×(yC-yP):![]() AE×(yC-yP)=BE:AE,
AE×(yC-yP)=BE:AE,
则BE:AE=3:5或5:3,
∵AB=|-1-3|=4
∴AE=![]() 或
或![]() ,
,
即:点E的坐标为(![]() ,0)或(
,0)或(![]() ,0),
,0),
设直线PC的解析式为:y=kx+b,
将点E(![]() ,0)、C(0,3)的坐标代入一次函数表达式得,
,0)、C(0,3)的坐标代入一次函数表达式得,
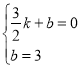 ,解得
,解得![]() ;
;
此时直线CP的表达式为:y=-2x+3;
将点E(![]() ,0)、C(0,3)的坐标代入一次函数表达式得,
,0)、C(0,3)的坐标代入一次函数表达式得,
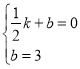 ,解得
,解得![]() ;
;
故直线CP的表达式为: y=-6x+3…②
联立①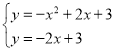 或
或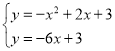
解①得:![]() 或
或 ![]() (不符合题意,舍去))
(不符合题意,舍去))
解②得:![]() 或
或 ![]() (不符合题意,舍去))
(不符合题意,舍去))
所以,点P的坐标为(4,-5)或(8,-45).

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.