Question

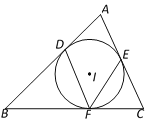
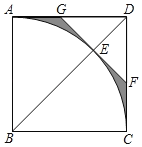
【题目】如图，在边长为2的正方形ABCD中，以B为圆心，AB为半径作扇形ABC，交对角线BD于点E，过点E作⊙B的切线分别交AD，CD于G，F两点，则图中阴影部分的面积为____．

Answer 1

【答案】．

【解析】

由四边形ABCD是正方形，且GF是⊙B的切线可证出△DGF是等腰直角三角形，再由正方形的边长可知BE的长，再求出DE的长，继而求出DG的长，再利用正方形面积－扇形面积－三角形面积即可求出阴影部分的面积．

∵四边形ABCD是正方形，

∴∠ABC=∠ADC=90°，∠GDE=∠FDE=45°．

∵GF是⊙B的切线，

∴BD⊥GF，

∴∠DEG=∠DEF=90°，

∴∠DGE=45°，∠DFE=45°，

∴DG=DF，GF=2DE，

∴DG=DFDE．

∵BDAB=2，

∴DE=BD﹣BE=22，

∴DG=DF(22)=4﹣2，

S阴影=S正方形ABCD﹣S扇形BAC﹣S△DGF

=2×2(4﹣2)2

=88﹣π．

故答案为：88﹣π．