Question

【题目】在正方形ABCD中，点E为对角线AC（不含点A）上任意一点，AB=；

（1）如图1，将△ADE绕点D逆时针旋转90°得到△DCF，连接EF；

①把图形补充完整（无需写画法）； ②求的取值范围；

(2)如图2，求BE+AE+DE的最小值．

Answer 1

【答案】（1）①补图见解析；②；（2）

【解析】

（1）①根据要求画出图形即可；

②首先证明∠ECF＝90°，设AE＝CF＝x，EF2＝y，则EC＝4x，在Rt△ECF中，利用勾股定理即可解决问题；

（2）如图2中，将△ABE绕点A顺时针旋转60°得到△AFG，连接EG，DF．作FH⊥AD于H．根据两点之间线段最短可得DF≤FG＋EG＋DE，BE＝FG，推出AE＋BE＋DE的最小值为线段DF的长；

（1）①如图△DCF即为所求；

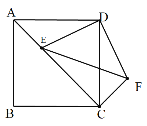
②∵四边形ABCD是正方形，

∴BC＝AB＝2，∠B＝90°，∠DAE＝∠ADC＝45°，

∴AC＝＝AB＝4，

∵△ADE绕点D逆时针旋转90°得到△DCF，

∴∠DCF＝∠DAE＝45°，AE＝CF，

∴∠ECF＝∠ACD＋∠DCF＝90°，

设AE＝CF＝x，EF2＝y，则EC＝4x，

∴y＝（4x）2＋x2＝2x28x＋160（0＜x≤4）．

即y＝2（x2）2＋8，

∵2＞0，

∴x＝2时，y有最小值，最小值为8，

当x＝4时，y最大值＝16，

∴8≤EF2≤16．

（2）如图中，将△ABE绕点A顺时针旋转60°得到△AFG，连接EG，DF．作FH⊥AD于H．

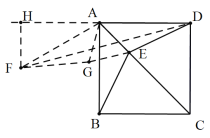
由旋转的性质可知，△AEG是等边三角形，

∴AE＝EG，

∵DF≤FG＋EG＋DE，BE＝FG，

∴AE＋BE＋DE的最小值为线段DF的长．

在Rt△AFH中，∠FAH＝30°，AB＝=AF，

∴FH＝AF＝，AH＝＝，

在Rt△DFH中，DF＝＝，

∴BE＋AE＋ED的最小值为．