题目内容
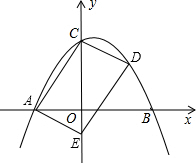
已知：如图，点A在y轴上，⊙A与x轴交于B、C两点，与y轴交于点D（0，3）和点E（0，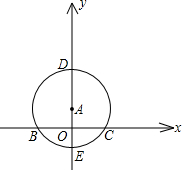
-1）
（1）求经过B、E、C三点的二次函数的解析式；
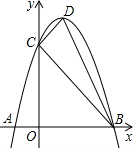
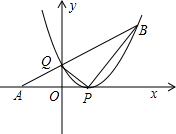
（2）若经过第一、二、三象限的一动直线切⊙A于点P（s，t），与x轴交于点M，连接PA并延长与⊙A交于点Q，设Q点的纵坐标为y，求y关于t的函数关系式，并观察图形写出自变量t的取值范围；
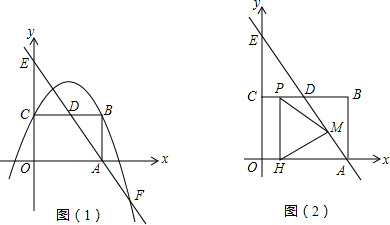
（3）在（2）的条件下，当y=0时，求切线PM的解析式，并借助函数图象，求出（1）中抛物线在切线PM下方的点的横坐标x的取值范围．
-1）（1）求经过B、E、C三点的二次函数的解析式；
（2）若经过第一、二、三象限的一动直线切⊙A于点P（s，t），与x轴交于点M，连接PA并延长与⊙A交于点Q，设Q点的纵坐标为y，求y关于t的函数关系式，并观察图形写出自变量t的取值范围；
（3）在（2）的条件下，当y=0时，求切线PM的解析式，并借助函数图象，求出（1）中抛物线在切线PM下方的点的横坐标x的取值范围．
（1）解法一：连接AC
∵DE为⊙A的直径，DE⊥BC
∴BO=CO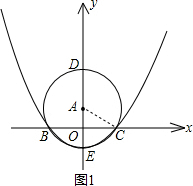
∵D（0，3），E（0，-1）
∴DE=|3-（-1）|=4，OE=1
∴AO=1，AC=
DE=2
在Rt△AOC中，AC2=AO2+OC2
∴OC=
∴C（
，0），B（
，0）
设经过B、E、C三点的抛物线的解析式为y=a(x-
)(x+
)，
则-1=a（0-
）（0+
）
解得a=
∴y=
（x-
）（x+
）=
x2-1（2分）．
解法二：∵DE为⊙A的直径，DE⊥BC
∴BO=CO
∴OC2=OD•OE
∵D（0，3），E（0，-1）
∴DO=3，OE=1
∴OC2=3×1=3
∴OC=
∴C（
，0），B（-
，0）
以下同解法一；
（2）解法一：过点P作PF⊥y轴于F，过点Q作QN⊥y轴于N
∴∠PFA=∠QNA=90°，F点的纵坐标为t
N点的纵坐标为y
∵∠PAF=∠QAN，PA=QA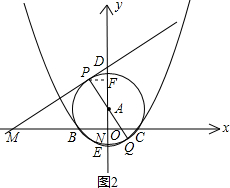
∴△PFA≌△QNA
∴FA=NA
∵AO=1
∴A（0，1）
∴|t-1|=|1-y|
∵动切线PM经过第一、二、三象限
观察图形可得1＜t＜3，-1＜y＜1．
∴t-1=1-y．
即y=-t+2．
∴y关于t的函数关系式为y=-t+2（1＜t＜3）（5分）
解法二：（i）当经过一、二、三象限的切线PM运动到使得Q点与C点重合时，y=0
连接PB
∵PC是直径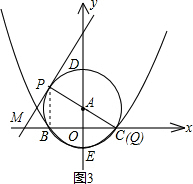
∴∠PBC=90°
∴PB⊥x轴，
∴PB=t．
∵PA=AC，BO=OC，AO=1，
∴PB=2AO=2，
∴t=2．
即t=2时，y=0．
（ii）当经过一、二、三象限的切线
PM运动使得Q点在x轴上方时，y＞0
观察图形可得1＜t＜2
过P作PS⊥x轴于S，过Q作QT⊥x轴于T
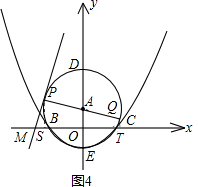
则PS∥AO∥QT
∵点A为线段PQ的中点
∴点O为线段ST的中点
∴AO为梯形QTSP的中位线
∴AO=
∴1=
∴y=-t+2．
∴y=-t+2（1＜t＜2）．
（iii）当经过一、二、三象限的切线PM运动使得Q点在x轴下方时，y＜0，观察图形可得2＜t＜3
过P作PS⊥x轴于S，过Q作QT⊥x轴于T，设PQ交x轴于R
则QT∥PS
∴△QRT∽△PRS
∴
=
设AR=m，则
=
&&（1）
又∵AO⊥x轴，
∴AO∥PS
∴△ROA∽△RSP
∴
=
∴
=
&&（2）
由（1）、（2）得y=-t+2
∴y=-t+2（2＜t＜3）
综上所述：y与t的函数关系式为y=-t+2（1＜t＜3）（5分）
（3）解法一：当y=0时，Q点与C点重合，连接PB
∵PC为⊙A的直径
∴∠PBC=90°
即PB⊥x轴
∴s=-
将y=0代入y=-t+2（1＜t＜3），得0=-t+2
∴t=2∴P（-
，2）
设切线PM与y轴交于点I，则AP⊥PI
∴∠API=9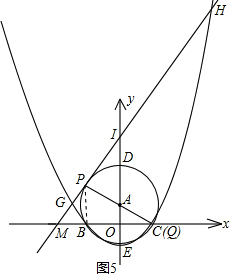
0°
在△API与△AOC中
∵∠API=∠AOC=90°，∠PAI=∠OAC
∴△API∽△AOC
∴
=
∴I点坐标为（0，5）
设切线PM的解析式为y=kx+5（k≠0），
∵P点的坐标为(-
，2)，
∴2=-
3 k+5．
解得k=
，
∴切线PM的解析式为y=
x+5（7分）
设切线PM与抛物线y=
x2-1交于G、H两点
由
可得x1=
，x2=
因此，G、H的横坐标分别为
、
根据图象可得抛物线在切线PM下方的点的横坐标x的取值范围是
＜x＜
（9分）
解法二：同（3）解法一
可得P（-
，2）
∵直线PM为⊙A的切线，PC为⊙A的直径
∴PC⊥PM
在Rt△CPM与Rt△CBP中
cos∠PCM=
=
∵CB=2
，PC=4
∴CM=
=
=
设M点的坐标为（m，0），
则CM=
-m=
∴m=-
．
即M（-
，0）．
设切线PM的解析式为y=kx+b（k≠0），
得
∵DE为⊙A的直径，DE⊥BC
∴BO=CO
∵D（0，3），E（0，-1）
∴DE=|3-（-1）|=4，OE=1
∴AO=1，AC=
| 1 |
| 2 |
在Rt△AOC中，AC2=AO2+OC2
∴OC=
| 3 |
∴C（
| 3 |
| 3 |
设经过B、E、C三点的抛物线的解析式为y=a(x-
| 3 |
| 3 |
则-1=a（0-
| 3 |
| 3 |
解得a=
| 1 |
| 3 |
∴y=
| 1 |
| 3 |
| 3 |
| 3 |
| 1 |
| 3 |
解法二：∵DE为⊙A的直径，DE⊥BC
∴BO=CO
∴OC2=OD•OE
∵D（0，3），E（0，-1）
∴DO=3，OE=1
∴OC2=3×1=3
∴OC=
| 3 |
∴C（
| 3 |
| 3 |
以下同解法一；
（2）解法一：过点P作PF⊥y轴于F，过点Q作QN⊥y轴于N
∴∠PFA=∠QNA=90°，F点的纵坐标为t
N点的纵坐标为y
∵∠PAF=∠QAN，PA=QA
∴△PFA≌△QNA
∴FA=NA
∵AO=1
∴A（0，1）
∴|t-1|=|1-y|
∵动切线PM经过第一、二、三象限
观察图形可得1＜t＜3，-1＜y＜1．
∴t-1=1-y．
即y=-t+2．
∴y关于t的函数关系式为y=-t+2（1＜t＜3）（5分）
解法二：（i）当经过一、二、三象限的切线PM运动到使得Q点与C点重合时，y=0
连接PB
∵PC是直径
∴∠PBC=90°
∴PB⊥x轴，
∴PB=t．
∵PA=AC，BO=OC，AO=1，
∴PB=2AO=2，
∴t=2．
即t=2时，y=0．
（ii）当经过一、二、三象限的切线
PM运动使得Q点在x轴上方时，y＞0
观察图形可得1＜t＜2
过P作PS⊥x轴于S，过Q作QT⊥x轴于T
则PS∥AO∥QT
∵点A为线段PQ的中点
∴点O为线段ST的中点
∴AO为梯形QTSP的中位线
∴AO=
| QT+PS |
| 2 |
∴1=
| y+t |
| 2 |
∴y=-t+2．
∴y=-t+2（1＜t＜2）．
（iii）当经过一、二、三象限的切线PM运动使得Q点在x轴下方时，y＜0，观察图形可得2＜t＜3
过P作PS⊥x轴于S，过Q作QT⊥x轴于T，设PQ交x轴于R
则QT∥PS
∴△QRT∽△PRS
∴
| QT |
| PS |
| QR |
| PR |
设AR=m，则
| -y |
| t |
| 2-m |
| 2+m |
又∵AO⊥x轴，
∴AO∥PS
∴△ROA∽△RSP
∴
| AO |
| PS |
| RA |
| RP |
∴
| 1 |
| t |
| m |
| 2+m |
由（1）、（2）得y=-t+2
∴y=-t+2（2＜t＜3）
综上所述：y与t的函数关系式为y=-t+2（1＜t＜3）（5分）
（3）解法一：当y=0时，Q点与C点重合，连接PB
∵PC为⊙A的直径
∴∠PBC=90°
即PB⊥x轴
∴s=-
| 3 |
将y=0代入y=-t+2（1＜t＜3），得0=-t+2
∴t=2∴P（-
| 3 |
设切线PM与y轴交于点I，则AP⊥PI
∴∠API=9
0°在△API与△AOC中
∵∠API=∠AOC=90°，∠PAI=∠OAC
∴△API∽△AOC
∴
| AP |
| AO |
| AI |
| AC |
∴I点坐标为（0，5）
设切线PM的解析式为y=kx+5（k≠0），
∵P点的坐标为(-
| 3 |
∴2=-
解得k=
| 3 |
∴切线PM的解析式为y=
| 3 |
设切线PM与抛物线y=
| 1 |
| 3 |
由
|
可得x1=
3
| ||||
| 2 |
3
| ||||
| 2 |
因此，G、H的横坐标分别为
3
| ||||
| 2 |
3
| ||||
| 2 |
根据图象可得抛物线在切线PM下方的点的横坐标x的取值范围是
3
| ||||
| 2 |
3
| ||||
| 2 |
解法二：同（3）解法一
可得P（-
| 3 |
∵直线PM为⊙A的切线，PC为⊙A的直径
∴PC⊥PM
在Rt△CPM与Rt△CBP中
cos∠PCM=
| PC |
| CM |
| CB |
| PC |
∵CB=2
| 3 |
∴CM=
| PC2 |
| CB |
| 16 | ||
2
|
8
| ||
| 3 |
设M点的坐标为（m，0），
则CM=
| 3 |
8
| ||
| 3 |
∴m=-
5
| ||
| 3 |
即M（-
5
| ||
| 3 |
设切线PM的解析式为y=kx+b（k≠0），
得
|
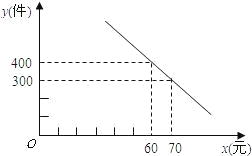间的函数关系式，并写出自变量x的取值范围；根据题意判断：当x取何值时，P的值最大，最大值是多少？
