题目内容
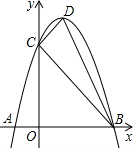
如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别相交于A(-1,0)、B(3,0)、C(0,3)三点,其顶点为D.(1)求:经过A、B、C三点的抛物线的解析式;
(2)求四边形ABDC的面积;
(3)试判断△BCD与△COA是否相似?若相似写出证明过程;若不相似,请说明理由.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(-
,
).
(2)求四边形ABDC的面积;
(3)试判断△BCD与△COA是否相似?若相似写出证明过程;若不相似,请说明理由.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |

(1)由题意,得
,
解之,得
,
∴y=-x2+2x+3;
(2)由(1)可知y=-(x-1)2+4,
∴顶点坐标为D(1,4),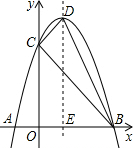
设其对称轴与x轴的交点为E,
∵S△AOC=
|AO|•|OC|,
=
×1×3,
=
,(5分)
S梯形OEDC=
(|DC|+|DE|)×|OE|,
=
(3+4)×1,
=
,
S△DEB=
|EB|•|DE|,
=
×2×4,
=4,(7分)
S四边形ABDC=S△AOC+S梯形OEDC+S△DEB,
=
+
+4,
=9;
(3)△DCB与△AOC相似,(9分)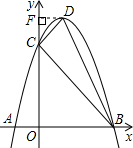
证明:过点D作y轴的垂线,垂足为F,
∵D(1,4),F(0,4),
∴Rt△DFC中,DC=
,且∠DCF=45°,
在Rt△BOC中,∠OCB=45°,BC=3
,
∴∠AOC=∠DCB=90°三角形相似,
=
=
,
∴△DCB∽△AOC.
|
解之,得
|
∴y=-x2+2x+3;
(2)由(1)可知y=-(x-1)2+4,
∴顶点坐标为D(1,4),

设其对称轴与x轴的交点为E,
∵S△AOC=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 3 |
| 2 |
S梯形OEDC=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 7 |
| 2 |
S△DEB=
| 1 |
| 2 |
=
| 1 |
| 2 |
=4,(7分)
S四边形ABDC=S△AOC+S梯形OEDC+S△DEB,
=
| 3 |
| 2 |
| 7 |
| 2 |
=9;
(3)△DCB与△AOC相似,(9分)

证明:过点D作y轴的垂线,垂足为F,
∵D(1,4),F(0,4),
∴Rt△DFC中,DC=
| 2 |
在Rt△BOC中,∠OCB=45°,BC=3
| 2 |
∴∠AOC=∠DCB=90°三角形相似,
| DC |
| AO |
| BC |
| CO |
| ||
| 1 |
∴△DCB∽△AOC.

练习册系列答案
相关题目
 点C,顶点为D.
点C,顶点为D.

 -1)
-1)
 若不是,请说明理由;
若不是,请说明理由;