题目内容
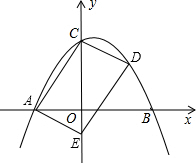
如图,抛物线y=-
x2+
x+6与x轴交于A、B两点,与y轴相交于C点.
(1)求△ABC的面积;
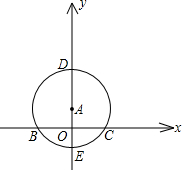
(2)已知E点(0,-3),在第一象限的抛物线上取点D,连接DE,使DE被x轴平分,试判定四边形ACDE的形状,并证明你的结论.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求△ABC的面积;
(2)已知E点(0,-3),在第一象限的抛物线上取点D,连接DE,使DE被x轴平分,试判定四边形ACDE的形状,并证明你的结论.

(1)根据抛物线的解析式可求得:A(-3,0),B(4,0),C(0,6)
S△ABC=
AB•OC=
×7×6=21.
(2)四边形ACDE是平行四边形,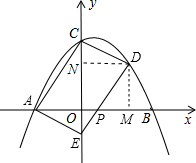
理由:设DE交x轴于点P.
作DM⊥x轴,DN⊥y轴,M、N是垂足.
在△EPO和△DPM中,
,
∴△EPO≌△DPM(AAS).
则DM=EO=3.点D的纵坐标为3.
由于D在抛物线上,则有3=-
x2+
x+6,
x=-2(舍去)或x=3.
因此:D(3,3),
AC=
=3
,ED=
=3
,
AE=
=3
,CD=
=3
,
AC=DE,AE=DC,
∴四边形ACDE是平行四边形.
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)四边形ACDE是平行四边形,

理由:设DE交x轴于点P.
作DM⊥x轴,DN⊥y轴,M、N是垂足.
在△EPO和△DPM中,
|
∴△EPO≌△DPM(AAS).
则DM=EO=3.点D的纵坐标为3.
由于D在抛物线上,则有3=-
| 1 |
| 2 |
| 1 |
| 2 |
x=-2(舍去)或x=3.
因此:D(3,3),
AC=
| OA2+OC2 |
| 5 |
| ND2+NE2 |
| 5 |
AE=
| AO2+OE2 |
| 2 |
| ND2+NC2 |
| 2 |
AC=DE,AE=DC,
∴四边形ACDE是平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
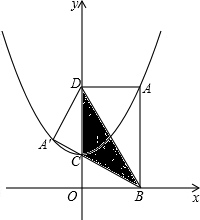

 -1)
-1)
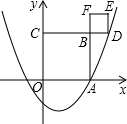 B交抛物线于点D,再以BD为边向上作正方形BDEF.
B交抛物线于点D,再以BD为边向上作正方形BDEF.