题目内容
【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)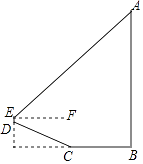
A.22.5 米
B.24.0 米
C.28.0 米
D.33.3 米
【答案】C
【解析】解:过点E作EM⊥AB与点M,
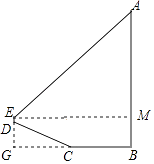
∵斜坡CD的坡度(或坡比)i=1:2.4,BC=CD=13米,
∴设CD=x,则CG=2.4x.
在Rt△CDG中,
∵DG2+CG2=DC2,即x2+(2.4x)2=132,解得x=5,
∴DG=5米,CG=12米,
∴EG=5+0.5=5.5米,BG=13+12=25米.
∵EM⊥AB,AB⊥BG,EG⊥BG,
∴四边形EGBM是矩形,
∴EM=BG=25米,BM=EG=5.5米.
在Rt△AEM中,
∵∠AEM=42°,
∴AM=EMtan42°≈25×0.90=22.5米,
∴AB=AM+BM=22.5+5.5=28米.
所以答案是:C.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目