题目内容
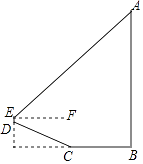
【题目】在△ABC中,AB=AC=![]() , BC=2,以AB
, BC=2,以AB![]() 为直径的⊙O分别交AC、BC于点D、E。
为直径的⊙O分别交AC、BC于点D、E。
(1)求证:E是BC的中点;
(2)连结DE,求证:△CDE∽△CBA;
(3)求△CDE的面积.
【答案】
(1)证明:连接AE,
∵AB为⊙O的直径,
∴∠AED=90°,
即AE⊥BC,
又∵AB=AC,
∴E为BC中点.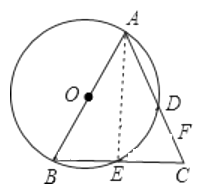
(2)证明:四边形是⊙O的内接四边形,
∴∠BED+∠BAD=180°,
又∵∠BED+∠DEC=180°,
∴∠BAD=∠DEC,
又∵∠BCA=∠DCE,
∴△CDE∽△CBA.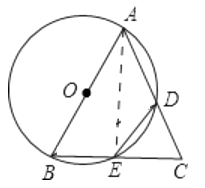
(3)解:由(1)知E为BC中点,
∵BC=2,
∴CE=BE=![]() BC=1,
BC=1,
由(2)知△CDE∽△CBA,
又∵AC=![]() ,
,
∴CE:CA=1:![]() ,
,
∴![]() =
=![]() ,
,
又由(1)知即AE⊥BC,
∴AE=![]() =2,
=2,
∴S△ABC=![]() .BC.AE=
.BC.AE=![]() ×2×2=2,
×2×2=2,
∴S△CDE=![]() S△ABC=
S△ABC=![]() ×2=
×2=![]() .
.
【解析】(1)连接AE,由圆周角定理得出∠AED=90°,又由等腰三角形的性质得出E为BC中点.
(2)由圆的内接四边形和邻补角定义得出∠BAD=∠DEC,又由∠BCA=∠DCE,根据相似三角形的判定:两个对应角相等的三角形相似即可得证.
(3)由(1)知E为BC中点,结合已知得出CE=BE=![]() BC=1,再结合勾股定理得出AE=
BC=1,再结合勾股定理得出AE=![]() =2,又由(2)知△CDE∽△CBA,根据相似三角形的性质得出
=2,又由(2)知△CDE∽△CBA,根据相似三角形的性质得出![]() =
=![]() ,由S△ABC=
,由S△ABC=![]() .BC.AE=
.BC.AE=![]() ×2×2=2,得出S△CDE=
×2×2=2,得出S△CDE=![]() S△ABC=
S△ABC=![]() ×2=
×2=![]() .
.
【考点精析】利用三角形的面积和等腰三角形的性质对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高;等腰三角形的两个底角相等(简称:等边对等角).

【题目】二次函数 ![]() ,自变量x与函数y的对应值如下表:
,自变量x与函数y的对应值如下表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
下列说法正确的是( )
A.抛物线的开口向下
B.当x>-3时,y随x的增大而增大
C.二次函数的最小值是-2
D.抛物线的对称轴x= ![]()