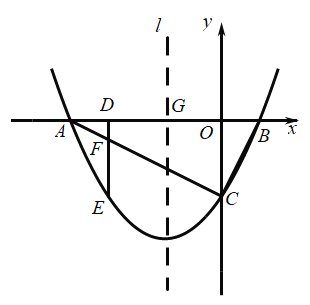题目内容
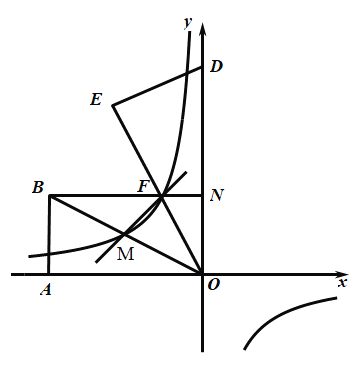
【题目】平面直角坐标系中,![]() 是等边三角形,点
是等边三角形,点![]() ,点
,点![]() ,点
,点![]() 是
是![]() 边上的一个动点(与点
边上的一个动点(与点![]() 、
、![]() 不重合).直线
不重合).直线![]() 是经过点
是经过点![]() 的一条直线,把
的一条直线,把![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 的对应点是点
的对应点是点![]() .
.
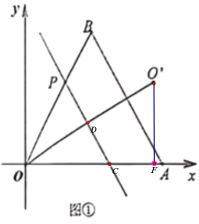
(1)如图①,当![]() 时,若直线
时,若直线![]() ,求点
,求点![]() 的坐标;
的坐标;
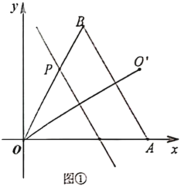
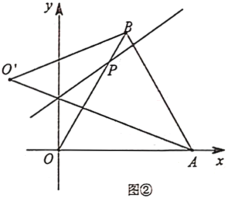
(2)如图②,当点![]() 在
在![]() 边上运动时,若直线
边上运动时,若直线![]() ,求
,求![]() 的面积;
的面积;
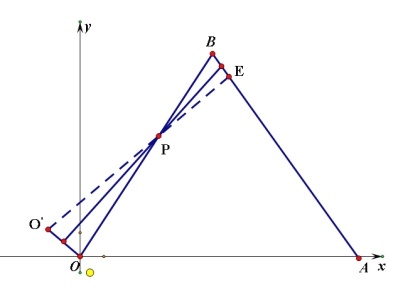
(3)当![]() 时,在直线
时,在直线![]() 变化过程中,求
变化过程中,求![]() 面积的最大值(直接写出结果即可).
面积的最大值(直接写出结果即可).
【答案】(1)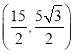 ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,再证明
,再证明![]() 是等边三角形;然后再根据
是等边三角形;然后再根据![]() ,
,![]() 、
、![]() 关于
关于![]() 对称,得到
对称,得到![]() ,
,![]() ;利用解直角三角形可以求得OD的长;过点
;利用解直角三角形可以求得OD的长;过点![]() 作
作![]() 于点
于点![]() ,在
,在![]() 中,解直角三角形可得OF和
中,解直角三角形可得OF和![]() 的长即可解答;
的长即可解答;
(2)连接![]() ,根据对称的性质和直线
,根据对称的性质和直线![]() 可得
可得![]() ,最后根据
,最后根据![]() 解答即可;
解答即可;
(3)作O’P⊥AB时,垂足为E,然后解三角形和线段的和差求得O’E,最后在运用三角形的面积公式求解即可.
解:(1)设直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∵![]() ,
,![]() ,
,![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]()
∵![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,在
,在![]() 中,可得
中,可得![]() ,
,
![]() ,
,
∴点![]() 的坐标为
的坐标为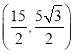
(2)连接![]() ,
,
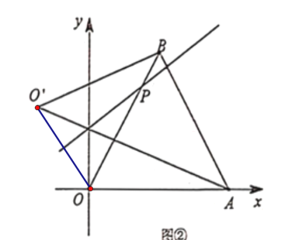
∵![]() ,
,![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() 直线
直线![]() ,
,
∵直线![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)当O’P⊥AB时,垂足为E,![]() 的面积最大
的面积最大
如图:作O’P⊥AB时,垂足为E
在Rt△BPE中,PA=2.∠B=60°
∴PE=PA·sin60°=![]()
∴O’E=6+![]() .
.
∴![]() 面积的最大值:
面积的最大值:![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目