题目内容
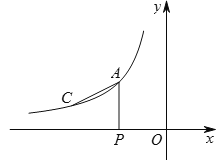
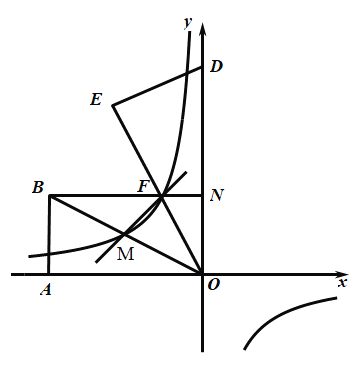
【题目】如图,![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在点
落在点![]() 处,得到
处,得到![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线交
轴的直线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.![]() ,
,![]() .
.
(1)求经过点![]() 、
、![]() 的反比例函数
的反比例函数![]() 和直线
和直线![]() :
:![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 轴,求五边形
轴,求五边形![]() 的面积;
的面积;
(3)直接写出当![]() 时
时![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据旋转可得![]() ,结合
,结合![]() 可得点
可得点![]() ,
,![]() ,再根据
,再根据![]() 可求得点
可求得点![]() ,从而求得
,从而求得![]() ,过点
,过点![]() 作
作![]() 轴,设
轴,设![]() ,根据
,根据![]() 过点
过点![]() 可得
可得![]() ,从而可得
,从而可得![]() ,由此再用待定系数法可求得
,由此再用待定系数法可求得![]() ;
;
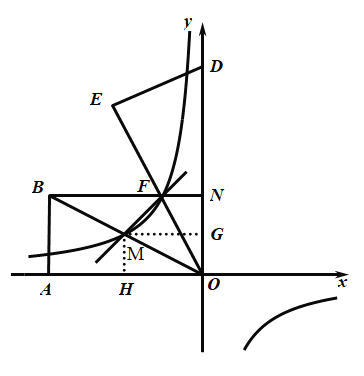
(2)过点![]() 作
作![]() ,则五边形
,则五边形![]() 的面积可转化为梯形NFMG和矩形GMHO的面积之和,再根据M、F的坐标为
的面积可转化为梯形NFMG和矩形GMHO的面积之和,再根据M、F的坐标为![]() 、
、![]() 即可求得相应的图形面积;
即可求得相应的图形面积;
(3)根据函数与不等式的关系,可得答案.
解:(1)由题意得:![]() ,
,
∴![]() ,
,
∴设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴点![]() ,
,
∵![]() 过点
过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() 轴,设
轴,设![]() ,
,
∴![]() 过点
过点![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() 过点
过点![]() 、
、![]() ,
,
∴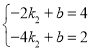 ,
,
![]() ,
,
∴![]() ,
,
(2)过点![]() 作
作![]() ,
,
∴![]()
![]() .
.
(3)从图象看,不等式![]() 的解集为:
的解集为:![]() 或
或![]() .
.

练习册系列答案
相关题目