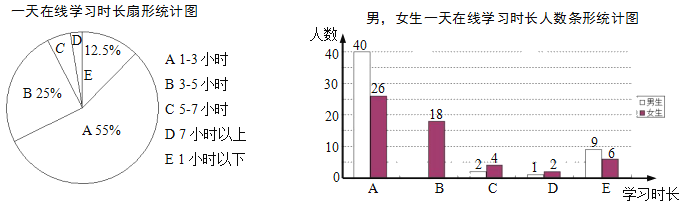
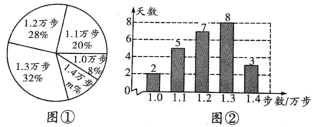
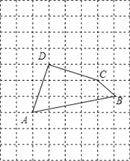
��Ŀ����
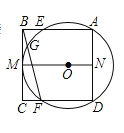
����Ŀ����֪����M��ƽ���ı���ABCD�Խ���AC����ֱ���ϵ�һ�����㣨��M�����A��C�غϣ����ֱ����A��C��ֱ��BM�����ߣ�����ֱ�Ϊ��E��F����OΪAC���е㣮
����ͼ1,����M���O�غ�ʱ��OE��OF��������ϵ�� ��
��ֱ��BM�Ƶ�B��ʱ�뷽����ת���ҡ�OFE=30����
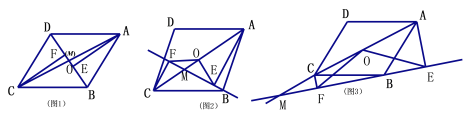
����ͼ2������M���߶�AC��ʱ�������߶�CF��AE��OE֮����������������ϵ������д����������֤����
����ͼ3������M���߶�AC���ӳ�����ʱ����ֱ��д���߶�CF��AE��OE֮���������ϵ��
���𰸡���1��OE=OF����2����![]() �������������CF=OE-AE
�������������CF=OE-AE
��������
��1���ɡ�AOE�ա�COF���ɵó����ۣ�
��2����ͼ2�еĽ���Ϊ��CF=OE+AE���ӳ�EO��CF�ڵ�N��ֻҪ֤����EOA�ա�NOC����OFN�ǵȱ������Σ����ɽ�����⣮
��ͼ3�еĽ���Ϊ��CF=OE-AE���ӳ�EO��FC���ӳ����ڵ�G��֤���������ƣ�
�⣺�š� ![]()
��AE��CF
��![]() ��
��![]() ,OA=OC
,OA=OC
���AOE�ա�COF.
��OE=OF��
�Ƣ� ![]()
�ӳ�EO��CF�ӳ�����N��

�� ![]()
��AE��CF
��![]() ��
��![]() ,OA=OC
,OA=OC
���OAE�ա�OCN
��AE=CN,OE=ON ��![]() ,
,![]()
��OF=ON=OE, ![]()
��OF=FN=ON=OE,��AE=CN
��CF=AE-OE
��CF=OE-AE,֤�����£�
�ӳ�EO��FC���ӳ����ڵ�G

�� ![]()
��AE��CF
���G=��AEO,��OCG=��EA0��
�֡�AO=OC��
���OAE�ա�OCG.
��AE=CG,OG=OE.
��![]() ,
,![]()
��OF=OG=OE, ![]()
���OGF�ǵȱ������Σ�
��FG=OF=OE.
��CF=OE-AE.

 ���ݼ���ϵ�д�
���ݼ���ϵ�д�