Question

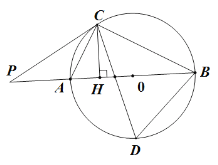
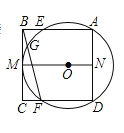
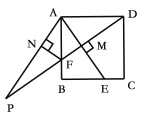
【题目】如图，正方形ABCD中，点E为BC边上的一点，连接AE，过点D作DM⊥AE，垂足为点M，交AB于点F．将△AMF沿AB翻折得到△ANF．延长DM，AN交于点P． 给出以下结论①；②；③；④若，则；．其中正确的是（　　）

A.①②③④B.①②③C.①②④D.③④

Answer 1

【答案】A

【解析】

根据正方形的性质和余角的性质证明∠BAE=∠ADM，从而得到△ABE≌△DAF，可判断①；再由翻折的性质证明∠FAN=∠FAM=∠ADM，从而可得，得到，可判断③；再由得到相似比，可得面积之比，可判断④.

解：∵四边形ABCD为正方形，

∴AD=AB，∠ABC=∠BAD=90°，

∴∠BAE+∠DAE=90°，

∵DM⊥AE，

∴∠DMA=90°，即∠ADM+∠DAM=90°，

∴∠BAE=∠ADM，

∴△ABE≌△DAF（AAS），故①正确；

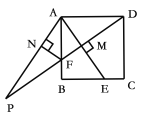
∵△ANF由△AMF翻折得到，

∴∠FAN=∠FAM=∠ADM，

∵∠P=∠P，

∴，故②正确；

∴，

∴，故③正确；

∵，

∴AF：AD=2:3,

则△APF和△DPA的相似比为2:3，

∴，

∴，故④正确.

故选A.