题目内容
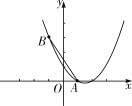
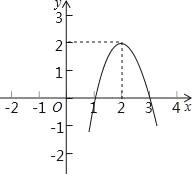
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
【答案】(1)x1=1,x2=3;(2)1<x<3;(3)k<2.
【解析】
(1)根据函数图象,二次函数图象与x轴的交点的横坐标即为方程的根;
(2)根据函数图象写出x轴上方部分的x的取值范围即可;
(3)能与函数图象有两个交点的所有k值即为所求的范围.
解:(1)∵函数图象与x轴的两个交点坐标为(1,0)(3,0),
∴方程的两个根为x1=1,x2=3;
(2)由图可知,不等式ax2+bx+c>0的解集为1<x<3;
(3)∵二次函数的顶点坐标为(2,2),
∴若方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为k<2.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
【题目】为参加 2020 年“陕西省初中毕业升学体育与健康考试”,小强同学进行了刻苦的训练.他在练习立定跳远时,测得其中 10 次立定跳远的成绩(单位:m)如下表:
成绩 | 2.25 | 2.33 | 2.35 | 2.41 | 2.42 |
次数 | 2 | 3 | 2 | 2 | 1 |
这 10 个数据的众数、中位数依次是( )
A.2.35,2.35B.2.33, 2.35C.3, 2.34D.2.33,2.34