题目内容
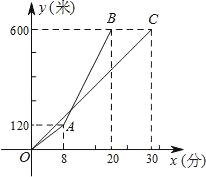
【题目】甲、乙两人沿同一路线登山，图中线段OC、折线OAB分别是甲、乙两人登山的路程y（米）与登山时间x（分）之间的函数图象．请根据图象所提供的信息，解答如下问题：
（1）求甲登山的路程与登山时间之间的函数关系式，并写出自变量x的取值范围；
（2）求乙出发后多长时间追上甲？此时乙所走的路程是多少米？
【答案】（1）y=20x（0≤x≤30）；（2）乙出发后10分钟追上甲，此时乙所走的路程是200米．
【解析】
试题（1）设甲登山的路程y与登山时间x之间的函数解析式为y=kx，根据图象得到点C的坐标，然后利用待定系数法求一次函数解析式解答；
（2）根据图形写出点A、B的坐标，再利用待定系数法求出线段AB的解析式，再与OC的解析式联立求解得到交点的坐标，即为相遇时的点．
试题解析：（1）设甲登山的路程y与登山时间x之间的函数解析式为y=kx，
∵点C（30，600）在函数y=kx的图象上，
∴600=30k，
解得k=20，
∴y=20x（0≤x≤30）；
（2）设乙在AB段登山的路程y与登山时间x之间的函数解析式为y=ax+b（8≤x≤20），
由图形可知，点A（8，120），B（20，600）
所以，
，解得
，所以，y=40x﹣200，
设点D为OC与AB的交点，联立
，解得
，
故乙出发后10分钟追上甲，此时乙所走的路程是200米．
练习册系列答案
相关题目
【题目】为了解某社区居民的用电情况，随机对该社区10户居民进行调查，下表是这10户居民2016年4月份用电量的调查结果：
居民（户） | 1 | 2 | 3 | 4 |
月用电量（度/户） | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量的说法错误的是（ ）
A.中位数是50
B.众数是51
C.平均数是46.8
D.方差是42
