题目内容
【题目】(阅读理解)
“若![]() 满足
满足![]() ,求
,求![]() 的值”
的值”
解:设![]() ,则
,则![]() ,
,
所以![]()
(解决问题)
(1)若![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
(2)若![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
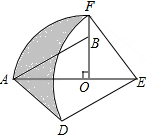
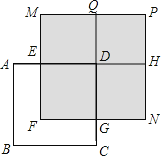
(3)如图,正方形![]() 的边长为
的边长为![]() ,
,![]() ,长方形
,长方形![]() 的面积是500,四边形
的面积是500,四边形![]() 和
和![]() 都是正方形,
都是正方形,![]() 是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).
是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).
【答案】(1)120;(2)2017;(3)2100
【解析】(1)根据举例进行解答即可;
(2)设(2017﹣x)=c,(2015﹣x)=d,则(2017﹣x)2+(2015﹣x)2=c2+d2=4038,c﹣d=(2017﹣x)﹣(2015﹣x)=2,所以2cd=(c2+d2)﹣(c﹣d)2=4038﹣22=4034,可得cd=2017,即可解答;
(3)根据正方形ABCD的边长为x,AE=10,CG=20,所以DE=(x﹣10),DG=x﹣20,得到(x﹣10)(x﹣20)=500,设(x﹣10)=a,(x﹣20)=b,从而得到ab=500,a﹣b=(x﹣10)﹣(x﹣20)=10,根据举例求出a2+b2,即可求出阴影部分的面积.
(1)设(30﹣x)=m,(x﹣20)=n,则(30﹣x)(x﹣20)=mn=﹣10,m+n=(30﹣x)+(x﹣20)=10,∴(30﹣x)2+(x﹣20)2=m2+n2=(m+n)2﹣2mn=(﹣10)2﹣2×(﹣10)=120;
(2)设(2017﹣x)=c,(2015﹣x)=d,则(2017﹣x)2+(2015﹣x)2=c2+d2=4038,c﹣d=(2017﹣x)﹣(2015﹣x)=2,2cd=(c2+d2)﹣(c﹣d)2=4038﹣22=4034,cd=2017,∴(2017﹣x)(2015﹣x)=cd=2017.
(3)∵正方形ABCD的边长为x,AE=10,CG=20,∴DE=(x﹣10),DG=x﹣20,∴(x﹣10)(x﹣20)=500,设(x﹣10)=a,(x﹣20)=b,∴ab=500,a﹣b=(x﹣10)﹣(x﹣20)=10,∴a2+b2=(a﹣b)2+2ab=102+2×500=1100,∴阴影部分的面积为:a2+b2+2ab=1100+2×500=2100.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案