Question

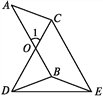
【题目】如图,线段AB=CD,AB与CD相交于点O,且∠1=60°,CE是由AB平移所得,试确定AC+BD与AB的大小关系,并说明理由.

Answer 1

【答案】AC+BD=AB或AC+BD>AB，理由见解析

【解析】试题分析：根据平移的基本性质得出AB与CE平行且相等，再根据三角形的三边关系得出BE+BD=AC+BD＞DE=AB解答即可．

试题解析：由平移的性质知，AB与CE平行且相等，

所以四边形ACEB是平行四边形，BE=AC，

当B、D、E不共线时，

∵AB∥CE，∠DCE=∠AOC=60°，

∵AB=CE，AB=CD，

∴CE=CD，

∴△CED是等边三角形，

∴DE=AB，

根据三角形的三边关系知BE+BD=AC+BD＞DE=AB，

即AC+BD＞AB．

当D、B、E共线时，AC+BD=AB．