题目内容
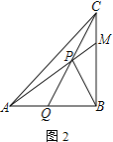
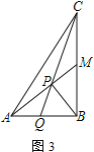
【题目】已知函数y=-x2+(m-1) x+m (m为常数),其顶点为M.
(1)请判断该函数的图像与x轴公共点的个数,并说明理由;
(2)当-2≤m≤3时,求该函数的图像的顶点M纵坐标的取值范围;
(3)在同一坐标系内两点A(-1,-1)、B(1,0),△ABM的面积为S,当m为何值时,S的面积最小?并求出这个最小值.
【答案】(1) 该函数的图像与![]() 轴公共点的个数是1个或2个;(2) 当-2≤m≤3时,该函数图像的顶点纵坐标的取值范围是0≤y≤4;(3) 当
轴公共点的个数是1个或2个;(2) 当-2≤m≤3时,该函数图像的顶点纵坐标的取值范围是0≤y≤4;(3) 当![]() 时,面积有最小值
时,面积有最小值![]()
【解析】
(1)计算判别式△的大小,比较与0的大小关系,即可得到根的个数,进而得到函数的图像与x轴公共点的个数;
(2)把函数的解析式化成顶点式,结合m的取值范围,即可得到图像的顶点M纵坐标的取值范围;
(3) 列出关于△ABM的面积为S的表达式,求其根据二次函数的性质求其最小值即可得到答案.
(1)由题意得:△=![]()
∴该函数的图像与![]() 轴公共点的个数是1个或2个 ;
轴公共点的个数是1个或2个 ;
(2)将y=-x2+(m-1) x+m化成顶点式得到
顶点的纵坐标是y=![]() ,
,
当m=-1时,y有最小值为0;
当m<﹣1时,y随m的增大而减小,
当m>﹣1时,y随m的增大而增大,
当m=-2时,y=0.25;
当m=3时,y=4,
则当-2≤m≤3时,该函数图像的顶点纵坐标的取值范围是0≤y≤4 ;
(3)根据题意,经过点M、点A的直线斜率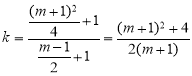
经过点M、点A的直线可表示为:![]()
令![]() 可得直线与x轴交点横坐标为
可得直线与x轴交点横坐标为![]()
则△ABM的面积为
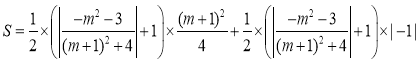
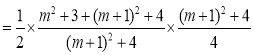
![]()
故当![]() 时,面积有最小值
时,面积有最小值![]() .
.

练习册系列答案
相关题目