Question

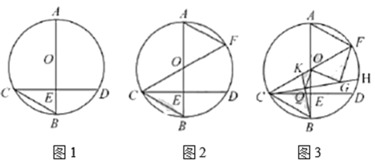
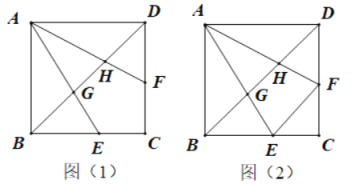
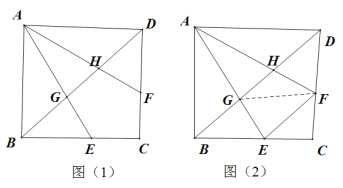
【题目】如图（1），已知正方形ABCD中，点E、F分别在边BC、CD上，BE=DF，AE、AF分别交BD于点G、H．

（1）求证：BG=DH；

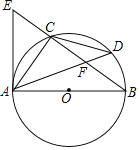
（2）连接FE，如图（2），当EF=BG时．

①求证：ADAH=AFDF；

②直接写出的比值．

Answer 1

【答案】(1)见解析； (2) ①见解析； ②

【解析】

（1）根据正方形性质证△ABE≌△ADF(SAS)，得∠BAE=∠DAF，再证△ABG≌△ADH(ASA)即可；

（2）①连接GF，证明四边形EBGF是平行四边形，利用BE∥GF∥AD，根据平行线分线段成比例性质可得：，，故.

②由①可得,,设CF=k,DF=a,根据勾股定理和 平行线分线段成比例性质得，得到，再代入化简可得.

证明：(1)∵四边形 ABCD为正方形

∴AB=AD,∠ABC=∠ADC

∵BE=DF

∴△ABE≌△ADF(SAS)

∴∠BAE=∠DAF

∵AB=AD

∴∠ABD=∠ADB

∴△ABG≌△ADH(ASA)

∴BG=DH

（2）①连接GF.

∵BC=DC,BE=DF，

∴CE=CF

∵∠C=90°

∴∠DBC=∠FEC=45°

∴EF∥BD

∵EF=BG

∴四边形EBGF是平行四边形

∴BE∥GF∥AD

∵AD=CD

∴

∵EF∥BD

∴

∴，即.

②由（2）可得

∴

∴

设CF=k,DF=a

则EF=，DG=，

∴DH= EF=，

∴GH=-

∴由可得

整理得

解得

∴

=