ЬтФПФкШн
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕxOyжаЕФЕуPКЭЁбMЃЈАыОЖЮЊrЃЉЃЌИјГіШчЯТЖЈвхЃКШєЕуPЙигкЕуMЕФЖдГЦЕуЮЊQЃЌЧвrЁмPQЁм3rЃЌдђГЦЕуPЮЊЁбMЕФГЦаФЕуЃЎ
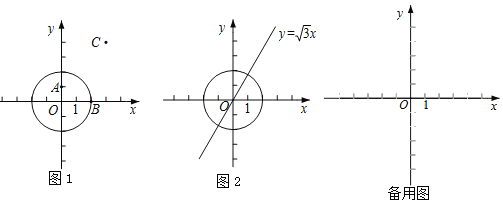
ЃЈ1ЃЉЕБЁбOЕФАыОЖЮЊ2ЪБЃЌ
ЂйШчЭМ1ЃЌдкЕуAЃЈ0ЃЌ1ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌCЃЈ3ЃЌ4ЃЉжаЃЌЁбOЕФГЦаФЕуЪЧЁЁ ЁЁЃЛ
ЂкШчЭМ2ЃЌЕуDдкжБЯпy![]() xЩЯЃЌШєЕуDЪЧЁбOЕФГЦаФЕуЃЌЧѓЕуDЕФКсзјБъmЕФШЁжЕЗЖЮЇЃЛ
xЩЯЃЌШєЕуDЪЧЁбOЕФГЦаФЕуЃЌЧѓЕуDЕФКсзјБъmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЁбTЕФдВаФЮЊTЃЈ0ЃЌtЃЉЃЌАыОЖЮЊ2ЃЌжБЯпy![]() x+1гыxжсЃЌyжсЗжБ№НЛгкЕуEЃЌFЃЎШєЯпЖЮEFЩЯЕФЫљгаЕуЖМЪЧЁбTЕФГЦаФЕуЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ
x+1гыxжсЃЌyжсЗжБ№НЛгкЕуEЃЌFЃЎШєЯпЖЮEFЩЯЕФЫљгаЕуЖМЪЧЁбTЕФГЦаФЕуЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁП(1)ЂйЕуAЃЌBЃЛЂк![]() m
m![]() Лђ
Лђ![]() m
m![]() ЃЛ(2) Љ2ЁмtЁм1
ЃЛ(2) Љ2ЁмtЁм1![]() Лђ2Ёмt
Лђ2Ёмt![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
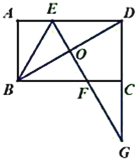
ЃЈ1ЃЉЂйЯШЧѓГіЕуAЃЌBЃЌCЙигкЕуOЕФЖдГЦЕуA'ЃЌB'ЃЌC'НјЖјЧѓГіAA'ЃЌBB'ЃЌCC'ЃЌдйХаЖЯМДПЩЕУГіНсТлЃЛ
ЂкЯШЧѓГіЕуDЕФзјБъЃЌдйРћгУаТЖЈвхНЈСЂВЛЕШЪНЧѓНтМДПЩЕУГіНсТлЃЛ
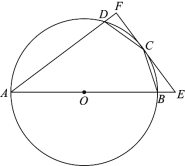
ЃЈ2ЃЉЯШЧѓГіЕуEЃЌFзјБъЃЌНјЖјЧѓГіЁЯEFO=60ЁуЃЌНјЖјевГіyжсЩЯЕНЯпЖЮEFЕФОрРыЮЊ2ЪБЕФЮЛжУЃЌдйЗжЧщПіРћгУаТЖЈвхЃЌМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЂйЁпAЃЈ0ЃЌ1ЃЉЃЌ
ЁрЕуAЙигкЕуOЕФЖдГЦЕуЮЊA'ЃЈ0ЃЌЉ1ЃЉЃЌ
ЁрAA'ЃН1ЉЃЈЉ1ЃЉЃН2ЃЌ
ЁпЁбOЕФАыОЖЮЊ2ЃЌ
ЁрЕуAЪЧЁбOЕФГЦаФЕуЃЌ
ЁпBЃЈ2ЃЌ0ЃЉЃЌ
ЁрЕуBЙигкЕуOЕФЖдГЦЕуЮЊB'ЃЈЉ2ЃЌ0ЃЉЃЌ
ЁрBB'ЃН2ЉЃЈЉ2ЃЉЃН4ЃЌ
ЁпЁбOЕФАыОЖЮЊ2ЃЌ
Ёр2ЃМBB'ЃМ6ЃЌ
ЁрЕуBЪЧЁбOЕФГЦаФЕуЃЌ
ЁпCЃЈ3ЃЌ4ЃЉЃЌ
ЁрЕуCЙигкЕуOЕФЖдГЦЕуЮЊC'ЃЈЉ3ЃЌЉ4ЃЉЃЌ
ЁрCC'![]() 25ЃО3rЃЌ
25ЃО3rЃЌ
ЁрЕуCВЛЪЧЁбOЕФГЦаФЕуЃЌ
ЙЪД№АИЮЊЃКЕуAЃЌBЃЛ
ЂкЁпЕуDдкжБЯпy![]() xЩЯЃЌЧвЕуDЕФКсзјБъЮЊmЃЌ
xЩЯЃЌЧвЕуDЕФКсзјБъЮЊmЃЌ
ЁрDЕФзјБъЮЊЃЈmЃЌ![]() mЃЉЃЌ
mЃЉЃЌ
ЁрЕуDЙигкЕуOЕФЖдГЦЕуD'ЕФзјБъЮЊЃЈЉmЃЌ![]() mЃЉЃЌ
mЃЉЃЌ
ЁрDD'![]() 4|m|ЃЌ
4|m|ЃЌ
ЁпЕуDЪЧЁбOЕФГЦаФЕуЃЌЧвЁбOЕФАыОЖЮЊ2ЃЌ
Ёр2Ём4|m|Ём6ЃЌ
Ёр![]() m
m![]() Лђ
Лђ![]() m
m![]() ЃЌ
ЃЌ
ЁрЕуDЕФКсзјБъmЕФШЁжЕЗЖЮЇЪЧ![]() m
m![]() Лђ
Лђ![]() m
m![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЃЌ
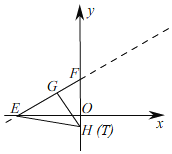
ЖдгкжБЯпy![]() x+1ЃЌ
x+1ЃЌ
СюxЃН0ЃЌ
ЁрyЃН1ЃЌFЃЈ0ЃЌ1ЃЉЃЌ
ЁрOFЃН1ЃЌ
СюyЃН0ЃЌ
Ёр![]() x+1ЃН0ЃЌ
x+1ЃН0ЃЌ
Ёрx![]() ЃЌ
ЃЌ
ЁрEЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁрOE![]() ЃЌ
ЃЌ
дкRtЁїEOFжаЃЌtanЁЯEFO![]() ЃЌ
ЃЌ
ЁрЁЯEFOЃН60ЁуЃЌ
Й§yжсЩЯвЛЕуHзїжБЯпEFЕФДЙЯпНЛЯпЖЮEFгкGЃЌ
ЁпЯпЖЮEFЩЯЕФЫљгаЕуЖМЪЧЁбTЕФГЦаФЕуЃЌЧвЁбTЕФАыОЖЮЊ2ЃЌ
ЁрTGзюаЁЃН2ЃЌ
дкRtЁїFGTжаЃЌsinЁЯEFO![]() ЃЌ
ЃЌ
ЁрFH![]() ЃЌ
ЃЌ
ЁрOHЃНFHЉOF![]() 1ЃЌ
1ЃЌ
ЕБЕуTДгHЯђЯТвЦЖЏЪБЃЌGHЃЌFHдНРДдНГЄЃЌEHдНРДдНЖЬЃЌЕНЕуGКЭEжиКЯжЎКѓЃЌGHдНРДдНГЄЃЌ
ЁпЯпЖЮEFЩЯЕФЫљгаЕуЖМЪЧЁбTЕФГЦаФЕуЃЌ
ЁрFHЃН1ЉtЁм3ЃЌ
ЁрtЁнЉ2ЃЌ
EHЁм3ЃЌ
Ёр![]() 3ЃЌ
3ЃЌ
Ёрt![]() ЃЌ
ЃЌ
ЁрЉ2ЁмtЁм1![]() ЃЌ
ЃЌ
ЕБЕуTДгЕуHЯђЩЯвЦЖЏЪБЃЌЕуTдкFHЩЯЪБЃЌTЕНEFЕФОрРыаЁгк2ЃЌДЫжжЧщПіВЛЗћКЯЬтвтЃЌ
ЕБЕуTДгЕуFЯђЩЯвЦЖЏЪБЃЌETЁнEFЃЌ
МДЃКETЁн2ЃЌ
ЁпЯпЖЮEFЩЯЕФЫљгаЕуЖМЪЧЁбTЕФГЦаФЕуЃЌ
ЁрFHЁн1ЃЌEHЁм3ЃЌ
ЁрtЉ1Ён1ЃЌ![]() 3ЃЌ
3ЃЌ
Ёр2Ёмt![]() ЃЌ
ЃЌ
ЧвtЕФШЁжЕЗЖЮЇЪЧЉ2ЁмtЁм1![]() Лђ2Ёмt
Лђ2Ёмt![]() ЃЎ
ЃЎ