题目内容
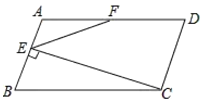
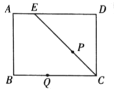
【题目】如图,矩形![]() 中,
中,![]() 对角线
对角线![]() 交于点
交于点![]() 为
为![]() 上任意点,
上任意点,![]() 为
为![]() 中点,则
中点,则![]() 的最小值为( )
的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
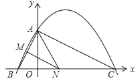
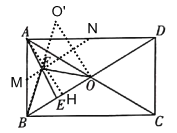
设M、N分别为AB、AD的中点,则MN是△ABD的中位线,点F在MN上,作点O关于MN的对称点O′,连接BO′,则BO′即为![]() 的最小值,易证△ABO是等边三角形,过点A作AH⊥BO于H,求出AH=OO′=
的最小值,易证△ABO是等边三角形,过点A作AH⊥BO于H,求出AH=OO′=![]() ,然后利用勾股定理求出BO′即可.
,然后利用勾股定理求出BO′即可.
解:如图,设M、N分别为AB、AD的中点,则MN是△ABD的中位线,
∵E为BD上任意点,F为AE中点,
∴点F在MN上,
作点O关于MN的对称点O′,连接BO′,则BO′即为![]() 的最小值,
的最小值,
∵四边形ABCD是矩形,![]() ,
,
∴OA=OB,∠AOB=60°,
∴△ABO是等边三角形,
∴AB=BO=4,
过点A作AH⊥BO于H,则BH=HO=2,
∴AH=![]() ,
,
∵MN∥BD,点H关于MN的对称点为A,点O关于MN的对称点为O′
∴OO′=AH=![]() ,且OO′⊥BD,
,且OO′⊥BD,
∴![]() ,
,
即![]() 的最小值为
的最小值为![]() ,
,
故选:A.

练习册系列答案
相关题目