Question

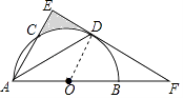
【题目】如图，AB为半圆O的直径，AC是⊙O的一条弦，D为 的中点，作DE⊥AC，交AB的延长线于点F，连接DA．
（1）求证：EF为半圆O的切线；
（2）若DA=DF=6 ，求阴影区域的面积．（结果保留根号和π）

Answer 1

【答案】
（1）证明：连接OD，

∵D为 的中点，

∴∠CAD=∠BAD，

∵OA=OD，

∴∠BAD=∠ADO，

∴∠CAD=∠ADO，

∵DE⊥AC，

∴∠E=90°，

∴∠CAD+∠EDA=90°，即∠ADO+∠EDA=90°，

∴OD⊥EF，

∴EF为半圆O的切线

（2）解：连接OC与CD，

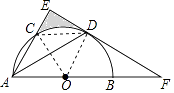
∵DA=DF，

∴∠BAD=∠F，

∴∠BAD=∠F=∠CAD，

又∵∠BAD+∠CAD+∠F=90°，

∴∠F=30°，∠BAC=60°，

∵OC=OA，

∴△AOC为等边三角形，

∴∠AOC=60°，∠COB=120°，

∵OD⊥EF，∠F=30°，

∴∠DOF=60°，

在Rt△ODF中，DF=6 ，

∴OD=DFtan30°=6，

在Rt△AED中，DA=6 ，∠CAD=30°，

∴DE=DAsin30 ，EA=DAcos30°=9，

∵∠COD=180°﹣∠AOC﹣∠DOF=60°，

∴CD∥AB，

故S△ACD=S△COD，

∴S阴影=S△AED﹣S扇形COD= ×9×3 ﹣ π×62= ﹣6π

【解析】（1）直接利用切线的判定方法结合圆心角定理分析得出OD⊥EF，即可得出答案；（2）直接利用得出S△ACD=S△COD ， 再利用S阴影=S△AED﹣S扇形COD ， 求出答案．
【考点精析】掌握扇形面积计算公式是解答本题的根本，需要知道在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．