题目内容
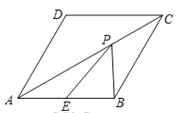
【题目】已知A、B、C三点在数轴上的位置如图所示，它们表示的数分别是a、b、c
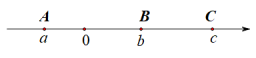
(1) 填空：abc________0，a＋b________ac，ab－ac________0；（填“＞”，“＝”或“＜”）
(2) 若|a|＝2，且点B到点A、C的距离相等
① 当b2＝16时，求c的值
② 求b、c之间的数量关系
③ P是数轴上B，C两点之间的一个动点设点P表示的数为x．当P点在运动过程中，bx＋cx＋|x－c|－10|x＋a|的值保持不变，求b的值
【答案】（1） < ， > ， > ；（2）①c=10；②c=2b+2；③b=3
【解析】
（1）根据点在数轴上的位置得到a＜0＜b＜c，于是得到结论；
（2）①根据已知条件达到a=-2，b=4，根据点B到点A，C的距离相等，列方程即可得到结论；
②根据
即可判断b、c之间的数量关系；
③依题意得原式=（b+c-11）x+10a+c当P点在运动过程中，原式的值保持不变，即原式的值与x无关，列方程组即可得到结论．
解：（1）由题中的数轴可知，a＜0＜b＜c，且
∴abc＜0，a+b＞0，ab-ac＞0，
故答案为：＜，＞，＞；
(2) ①
且
,
,
且
,
.
∵点B到点A，C的距离相等,∴
∴
,∴
②∵, ∴
,
③依题意，得
∴原式=
∵
∴原式=
【此处
不取-2没关系】
∵当 P 点在运动过程中，原式的值保持不变，即原式的值与
无关
∴
,∴
.
阅读快车系列答案【题目】在太空种子种植体验实践活动中，为了解“宇番2号”番茄，某校科技小组随机调查60株番茄的挂果数量x（单位：个），并绘制如下不完整的统计图表：
“宇番2号”番茄挂果数量统计表
挂果数量x（个） | 频数（株） | 频率 |
25≤x＜35 | 6 | 0.1 |
35≤x＜45 | 12 | 0.2 |
45≤x＜55 | a | 0.25 |
55≤x＜65 | 18 | b |
65≤x＜75 | 9 | 0.15 |
请结合图表中的信息解答下列问题：
（1）统计表中，a= ，b= ；
（2）将频数分布直方图补充完整；
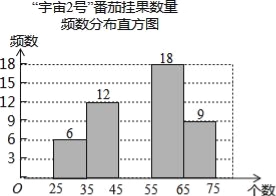
（3）若绘制“番茄挂果数量扇形统计图”，则挂果数量在“35≤x＜45”所对应扇形的圆心角度数为 °；
（4）若所种植的“宇番2号”番茄有1000株，则可以估计挂果数量在“55≤x＜65”范围的番茄有 株．
【题目】某淘宝商家计划平均每天销售某品牌儿童滑板车100辆，但由于种种原因，实际每天的销售量与计划量相比有出入。下表是某周的销售情况（超额记为正、不足记为负）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 | +4 | -3 | -5 | +14 | -8 | +21 | -6 |
（1）根据记录的数据可知该店前三天共销售该品牌儿童滑板车______辆。
（2）根据记录的数据可知销售量最多的一天比销售量最少的一天多销售______辆。
（3）该店实行每日计件工资制，每销售一辆车可得40元，若超额完成任务，则超过部分每辆另奖15元；少销售一辆扣20元，那么该店铺的销售人员这一周的工资总额是多少元？
