题目内容
【题目】如图,在同一平面内,∠AOB=150°,∠COD=90°,OE平分∠BOD.
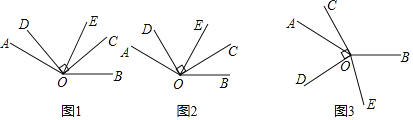
(1)当∠COD的位置如图1所示时,若∠COE=25°,则∠AOD= ;
(2)当∠COD的位置如图2所示时,若∠AOE=90°,则∠AOD= ;
(3)当∠COD的位置如图3所示时,若∠BOE=![]() ∠AOC,求∠AOD的度数.
∠AOC,求∠AOD的度数.
【答案】(1)20°(2)30°(3)60°.
【解析】
(1)根据角平分线的定义与角的和差即可得到结论;
(2)根据角平分线的定义与角的和差即可得到结论;
(3)根据余角的性质和角平分线的定义以及角的倍分关系列方程解答即可得到结论.
(1)∵∠COD=90°,∠COE=25°,
∴∠EOD=65°,
∵OE平分∠BOD,
∴∠BOD=2∠EOD=130°,
∴∠AOD=∠AOB﹣∠BOD=20°;
故答案为:20°
(2)∵∠COD=90°,∠AOE=90°,
∴∠COE+∠DOE=90°,∠AOD+∠DOE=90°,
∴∠AOD=∠COE,
设∠AOD![]() ,则∠COE
,则∠COE![]()
∴∠BOC=∠AOB-∠AOE-![]() =150
=150![]() -90
-90![]() -
-![]() =
=![]() -
-![]() ,
,
∵OE平分∠BOD,
∴∠DOE=∠BOE=![]() ,
,
∵∠AOD+∠DOE=90°,
∴∠AOD=90°-![]() =30°.
=30°.
故答案为:30°
(3)因为OE平分∠BOD
所以∠BOE=∠DOE
因为∠BOE=![]() ∠AOC
∠AOC
所以∠BOD=5∠AOC
因为∠COD=90°,所以∠AOD+∠AOC=90°
设∠AOC=x,
则∠AOD=90°﹣x,∠BOD=5x,
因为∠AOD+∠BOD+∠AOB=360°
所以90°﹣x+5x+150°=360°,
解得:x=30°,
所以∠AOD=90°﹣x=90°﹣30°=60°,
即∠AOD的度数是60°.

【题目】小明同学对平面图形进行了自主探究;图形的顶点数A,被分成的区域数B,线段数C三者之间是否存在确定的数量关系.如图是他在探究时画出的5个图形.
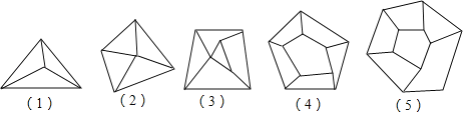
(1)根据图完成表格:
A | B | C | |
平面图形(1) |
| 3 | 6 |
平面图形(2) | 5 |
| 8 |
平面图形(4) | 10 | 6 |
|
(2)猜想:一个平面图形中顶点数A,区域数B,线段数C之间的数量关系是 ;
(3)计算:已知一个平面图形有24条线段,被分成9个区域,则这个平面图形的顶点有 个.