题目内容
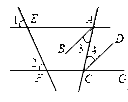
【题目】如图,在⊙O中,B,P,A,C是圆上的点,PB= PC, PD⊥CD,CD交⊙O于A,若AC=AD,PD =![]() ,sin∠PAD =
,sin∠PAD =![]() ,则△PAB的面积为_______.
,则△PAB的面积为_______.
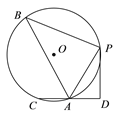
【答案】2
【解析】分析: 连接PC PB PA,过P做BA垂线于H点,根据PB=PC,再由全等三角形的判定定理可得出△PBH≌△PCD,Rt△PHA≌Rt△PDA,根据AC=AD=1即可得出结论.
详解: 连接PC PB PA,过P做BA垂线于H点,
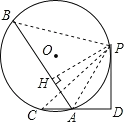
∵PD⊥CD, PD =![]() ,sin∠PAD =
,sin∠PAD =![]() ,
,
∴AP=![]() ,AD=1,
,AD=1,
∵AC=AD,
∴CD=2.
在△PBH与△PCD中,
∠B=∠C
PB=PC
∠BPH=∠DPC,
∴△PBH≌△PCD(ASA),
∴BH=CD=2,PH=PD=![]() ,
,
∴AH=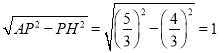 ,
,
∴△PAB的面积为AB×PH×![]() =(2+1)×
=(2+1)×![]() ×
×![]() =2,
=2,
故答案为:2.
点睛:
本题考查的是圆周角定理及全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

 习题精选系列答案
习题精选系列答案【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?