题目内容
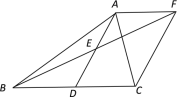
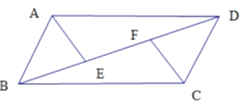
【题目】如图,在口ABCD中,点E、F是对角线BD上的两点,且BF=DE,连接AE、CF.
.求证:AE//CF.
【答案】证明见解析
【解析】试题分析:根据平行四边形的性质可得AD=CB,∠ADE=∠CBF,利用SAS判定△ADE≌△CBF,根据全等三角形的性质即可得∠AED=∠BFC,所以AE∥CF.
试题解析:
∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,
∴∠ADE=∠CBF,
又∵DE=BF,
∴△ADE≌△CBF,
∴∠AED=∠BFC,
∴AE∥CF.
【题型】解答题
【结束】
22
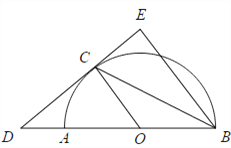
【题目】如图,已知![]() 是
是![]() 的直径,CD与
的直径,CD与![]() 相切于C,
相切于C, ![]() .
.
(1)求证:BC 是![]() 的平分线.
的平分线.
(2)若DC=8, ![]() 的半径OA=6,求CE的长.
的半径OA=6,求CE的长.
【答案】(1)证明见解析;(2)4.8
【解析】分析:(1)由![]() ,推出
,推出![]() ,由
,由![]() ,推出
,推出![]() ,可得
,可得![]() .(2)在
.(2)在![]() 中,求出OD,由
中,求出OD,由![]() ,可得
,可得![]() ,由此即可解决问题.
,由此即可解决问题.
详解:(1)证明:因为![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
故可得![]() ,
,
即可得![]() 是
是![]() 的平分线.
的平分线.
(2)因为DE是![]() 的切线,
的切线,
所以![]() ,即在
,即在![]() 中,DC=8,OC=OA=6,所以
中,DC=8,OC=OA=6,所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
即可得EC=4.8

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
【题目】小明同学对平面图形进行了自主探究;图形的顶点数A,被分成的区域数B,线段数C三者之间是否存在确定的数量关系.如图是他在探究时画出的5个图形.
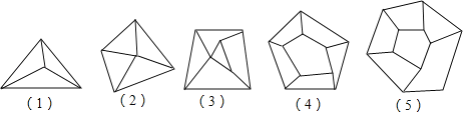
(1)根据图完成表格:
A | B | C | |
平面图形(1) |
| 3 | 6 |
平面图形(2) | 5 |
| 8 |
平面图形(4) | 10 | 6 |
|
(2)猜想:一个平面图形中顶点数A,区域数B,线段数C之间的数量关系是 ;
(3)计算:已知一个平面图形有24条线段,被分成9个区域,则这个平面图形的顶点有 个.