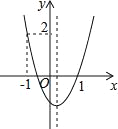��Ŀ����
����Ŀ����ͼ��ֱ������ϵ�У�ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ����A��B���㣬��֪A�����������2.
��ͼ����A��B���㣬��֪A�����������2.
��1�����������Ľ���ʽ.
��2����ֱ��![]() ��x������ƽ��6����λ���뷴���������ڵڶ������ڽ��ڵ�C.����P��y�����������˶������߶�PA���߶�PC֮��ﵽ���ʱ�����P������.
��x������ƽ��6����λ���뷴���������ڵڶ������ڽ��ڵ�C.����P��y�����������˶������߶�PA���߶�PC֮��ﵽ���ʱ�����P������.

���𰸡���1��![]() ����2��P��0,6��
����2��P��0,6��
�������������������1������õ�A�����꣬�����ô���ϵ������÷����������Ľ���ʽ���ɣ���2������AC����������������֮��С�ڵ�����֪����A��C��P������ʱ��PA-PC<AC����A��C��P������ʱ��PA-PC=AC����ˣ�����P��ֱ��AC��y��Ľ���ʱ��PA-PCȡ�����ֵ.�����ƽ�ƺ�ֱ�ߵĽ���ʽ�������ƽ�ƺ�ֱ���뷴����������ͼ��Ľ������꣬�����ֱ��AC�Ľ���ʽ��������õ�P������.
���������
![]() ��һ�κ���
��һ�κ���![]() ��
��![]() ����
����![]() ��
��
��ã�![]() ������A������Ϊ��-4��2����
������A��������-4��2����
����A��-4��2���ڷ���������![]() ��ͼ���ϣ�
��ͼ���ϣ�
��k=-4��2=-8��
�෴���������ı���ʽΪ![]() ��
��
![]() ����AC����������������֮��С�ڵ�����֪����A��C��P������ʱ��PA-PC<AC����A��C��P������ʱ��PA-PC=AC����ˣ�����P��ֱ��AC��y��Ľ���ʱ��PA-PCȡ�����ֵ.
����AC����������������֮��С�ڵ�����֪����A��C��P������ʱ��PA-PC<AC����A��C��P������ʱ��PA-PC=AC����ˣ�����P��ֱ��AC��y��Ľ���ʱ��PA-PCȡ�����ֵ.
��ƽ�ƺ�ֱ����x�ύ�ڵ�F����F��6��0��
��ƽ�ƺ��ֱ�߽���ʽΪ![]() ��
��
��F��6��0������![]() �ã�b=3
�ã�b=3
��ֱ��CF����ʽ��![]()
��![]() 3=
3=![]() ����ã�
����ã�![]() ��
��
��C��-2��4��
��A��C��������ֱ�ΪA��-4��2����C��-2��4��
��ֱ��AC�ı���ʽΪ![]() ��
��
��ʱ��P������ΪP��0��6��.
�㾦��������һ�κ����뷴�����������ۺ��⣬��Ҫ�������ô���ϵ���������Ľ���ʽ��һ�κ����뷴���������Ľ������꣬��������һ�κ����������������������ǽ���Ĺؼ�.
�����͡������
��������
26
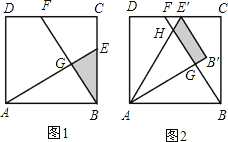
����Ŀ�����ı���ABCD�ı�AB��ADΪ�ױ߷ֱ�������������ABF��ADE,����EB.
(1)���ı���ABCDΪ������ʱ(��ͼ1),�Ա�AB��ADΪб�߷ֱ������������ֱ��������ABF��ADE������EB��FD���߶�EB��FD��������ϵ�� .
(2)���ı���ABCDΪ����ʱ(��ͼ2),�Ա�AB��ADΪб�߷ֱ����ڲ�������ֱ��������ABF��ADE������EF��BD���߶�EF��BD����������������ϵ?�����֤��;
(3)���ı���ABCDΪƽ���ı���ʱ(��ͼ3),�Ա�AB��ADΪб�߷ֱ���ƽ���ı����ڲ⡢���������ֱ��������ABF��ADE������EAD����FBA�Ķ��Ƕ�Ϊ��������EF��BD������ΪG����������ʾ����EGD����˵������.
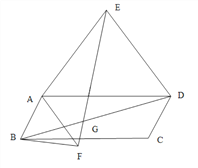
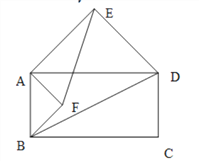

ͼ1 ͼ2 ͼ3
���𰸡���1��EF=BD����2��EF=![]() BD����3��
BD����3��![]()
����������������1�������ε����ʡ��ȱ������ε����ʺ�ȫ�������ε�֤��������֤����AFD�ա�ABE����ȫ�������ε����ʼ��ɵõ�EB=FD����2�����ݵ���ֱ�������ε����ʿɵ�![]() ����֤�á�BAD=��FAE�������ж���BAD����FAE ���������������ε����ʿɵ�
����֤�á�BAD=��FAE�������ж���BAD����FAE ���������������ε����ʿɵ�![]() �����ɵ�
�����ɵ�![]() ����3��
����3��![]() ����֤��BFA����DEA�����ɵ�
����֤��BFA����DEA�����ɵ�![]() ��
��
��֤��![]() �����ԡ�BAD����FAE������ȫ�������ε����ʼ��ɵ�
�����ԡ�BAD����FAE������ȫ�������ε����ʼ��ɵ�![]() �����ɡ�AHE=��DHG�����ɵ�
�����ɡ�AHE=��DHG�����ɵ�![]() .
.
��⣺(1)EF=BD��
�������£�
�ı���ABCDΪ�����Σ�
��AB=AD��
�����ı���ABCD�ı�AB��ADΪ�߷ֱ���������ȱ�������ABF��ADE��
��AF=AE����FAB=��EAD=60����
�ߡ�FAD=��BAD+��FAB=90��+60��=150����
��BAE=��BAD+��EAD=90��+60��=150����
���FAD=��BAE��
�ڡ�AFD�͡�ABE�У� 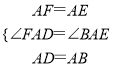 ��
��
���AFD�ա�ABE��
��EB=FD��
(2)EF=![]() BD.
BD.
֤�����ߡ�AFBΪ����ֱ��������
��![]() ,��FAB=45��
,��FAB=45��
ͬ���� ![]() ,��EAD=45�� ���BAD+��FAD=��EAD+��DAF
,��EAD=45�� ���BAD+��FAD=��EAD+��DAF
����BAD=��FAE
��![]() ��
�� ![]() ��
��![]()
���BAD����FAE ��![]()
���� ![]()
��3���⣺ ![]()
�ߡ�AFBΪ����ֱ������������FB=FA��
ͬ����ED=EA����![]() ��
��
�֡�![]() �����BFA����DEA��
�����BFA����DEA��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���BAD����FAE��
��![]() ��
��
�֡ߡ�AHE=��DHG��
��![]() .
.

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д�����Ŀ��ijУ���꼶ѧ��С����Сǿ��С�쵽ij���вμ������ʵ������ڻ�����Dz�����ij��ˮ�������۹�������֪��ˮ���Ľ���Ϊ8Ԫ/ǧ�ˣ������������ڻ������ĶԻ���
С���������10Ԫ/ǧ�˵ļ۸����ۣ���ôÿ����۳�300ǧ�ˣ�
Сǿ�����ÿǧ�˵�����Ϊ3Ԫ����ôÿ����۳�250ǧ�ˣ�
С�죺�����13Ԫ/ǧ�˵ļ۸����ۣ���ôÿ��ɻ�ȡ����750Ԫ��
������=�����ۼ�-���ۣ�![]() ��������
��������
��1����������ǵĶԻ���д�±���
���۵���x��Ԫ/kg�� | 10 | 11 | 13 |
������y��kg�� |
��2��������ݱ����е���Ϣ�ж�ÿ���������y��ǧ�ˣ������۵���x��Ԫ��֮����������ĺ�����ϵ������y��ǧ�ˣ���x��Ԫ����x��0���ĺ�����ϵʽ��
��3����ó�����������ˮ��ÿ���ȡ������ΪWԪ����W��x�ĺ�����ϵʽ�������۵���Ϊ��ֵʱ��ÿ��ɻ�õ����������������Ƕ���Ԫ��