题目内容
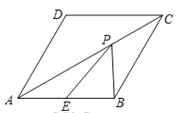
【题目】如图，在菱形
中，
=120°，点E是边
的中点，P是对角线
上的一个动点，若AB=2，则PB+PE的最小值是（ ）
A. 1B. 
C. 2D. 
【答案】B
【解析】
找出B点关于AC的对称点D，连接DE交AC于P，则DE就是PB
+PE的最小值，求出即可.
解：连接DE交AC于P，连接DE，DB，
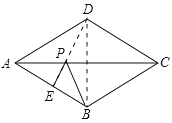
由菱形的对角线互相垂直平分，可得B、D关于AC对称，则PD=PB，
∴PE+PB=PE+PD=DE，
即DE就是PE+PB的最小值，
∵∠ABC=120°，
∴∠BAD=60°，
∵AD=AB，
∴△ABC是等边三角形，
∵AE=BE，
∴DE⊥AB（等腰三角形三线合一的性质）.
在Rt△ADE中，DE=
=
.
即PB+PE的直线值为.
故选：B.
“点睛”本题主要考查轴对称. 最短路线问题，勾股定理等知识点。确定P点的位置是解答此题的关键.
练习册系列答案
相关题目
