题目内容
【题目】如图,已知四边形ABCD的顶点为A(1,2),B(﹣1,2),C(﹣1,﹣2),D(1,﹣2).点M和点N同时从E点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2016次相遇时的坐标为_____.
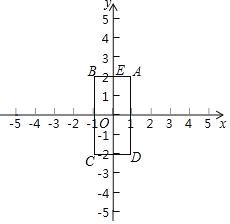
【答案】(0,2).
【解析】
由点A、B、C、D的坐标可得出AB、BC的长度,设点M和点N第2016次相遇时的时间为x,根据第一次相遇的路程和=周长,所以第2016次相遇的路程和=周长×2016,即可得出关于x的一元一次方程,解之即可得出x的值,再根据路程=速度×时间可求出M和点N第2016次相遇时,点M走过的路程,结合矩形的周长为12,即可找出点M和点N第2016次相遇时的坐标,此题得解.
解:∵A(1,2),B(﹣1,2),C(﹣1,﹣2),D(1,﹣2),
∴AB=2,BC=4.
设点M和点N第2016次相遇时的时间为x,
根据题意得:(1+2)x=2016×2×(4+2),
解得:x=8064,
∴M和点N第2016次相遇时,点M走过的路程为x=8064.
∵矩形ABCD的周长为12,8064=672×12,
∴M和点N第2016次相遇时的位置在点E.
∴点M和点N第2016次相遇时的位置为线段CF的中点,即点(0,2).
故答案为:(0,2).

【题目】为了迎接“六一”儿童节.某儿童运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋 价格 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?该专卖店要获得最大利润应如何进货?