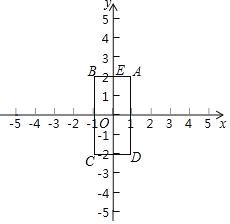Question

【题目】(1)观察猜想

如图①,点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°，AD=AE,则BC、BD、CE之间的数量关系为

(2)问题解决

如图②,在Rt△ABC中,∠ABC=90°，CB=8，AB=4，以AC为直角边向外作等腰Rt△DAC连接BD,求BD的长。

(3)拓展延伸

如图③,在四边形ABCD中,∠ABC=∠ADC=90°，CB=8.AB=4，DC=DA，则BD=

Answer 1

【答案】（1）；

（2）；

（3）.

【解析】

（1）观察猜想：证明△ADB≌△EAC，可得结论：BC=AB+AC=BD+CE；
（2）问题解决：作辅助线，同理证明：△ABC≌△DEA，可得DE=AB=2，AE=BC=4，最后利用勾股定理求BD的长；
（3）拓展延伸：同理证明三角形全等，设AF=x，DF=y，根据全等三角形对应边相等列方程组可得结论．

解：（1）观察猜想
BC=BD+CE，

理由是：如图①，∵∠B=90°，∠DAE=90°，
∴∠D+∠DAB=∠DAB+∠EAC=90°，
∴∠D=∠EAC，
∵∠B=∠C=90°，AD=AE，
∴△ADB≌△EAC（AAS），
∴BD=AC，EC=AB，
∴BC=AB+AC=BD+CE；

（2）问题解决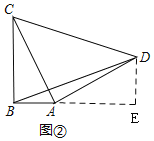

如图②，过D作DE⊥AB，交BA的延长线于E，
由（1）得：△ABC≌△DEA，
∴DE=AB=4，AE=BC=8，
Rt△BDE中，BE=BA+AE=4+8=12，

由勾股定理得：

（3）拓展延伸

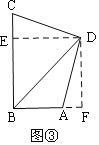
如图③，过D作DE⊥BC于E，作DF⊥AB于F，
同理得：△CED≌△AFD，
∴CE=AF，ED=DF，
设AF=x，DF=y，

∵BC=8，AB=4，

则，解得： ，

∴BF=AF+ AB=2+4=6，DF=6，
由勾股定理得：．