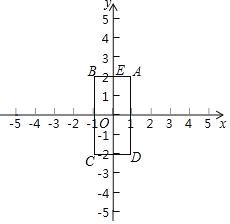题目内容
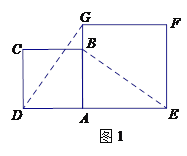
【题目】(本题满分12分)在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为![]() 的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现![]() ,请你帮他说明理由.
,请你帮他说明理由.
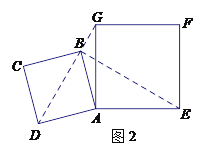
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
(3)如图3,若小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△![]() 与△
与△![]() 面积之和的最大值,并简要说明理由.
面积之和的最大值,并简要说明理由.
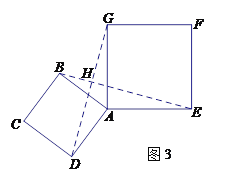
【答案】(1)见解析;(2)![]() (3)6
(3)6
【解析】
试题(1)由四边形ABCD与四边形AEFG为正方形,利用正方形的性质得到两对边相等,且夹角相等,利用SAS得到三角形ADG与三角形ABE全等,利用全等三角形对应角相等得∠AGD=∠AEB,如图1所示,延长EB交DG于点H,利用等角的余角相等得到∠DHE=90°,利用垂直的定义即可得DG⊥BE;
(2)由四边形ABCD与四边形AEFG为正方形,利用正方形的性质得到两对边相等,且夹角相等,利用SAS得到三角形ADG与三角形ABE全等,利用全等三角形对应边相等得到DG=BE,如图2,过点A作AM⊥DG交DG于点M,∠AMD=∠AMG=90°,在直角三角形AMD中,求出AM的长,即为DM的长,根据勾股定理求出GM的长,进而确定出DG的长,即为BE的长;
(3)△GHE和△BHD面积之和的最大值为6,理由为:对于△EGH,点H在以EG为直径的圆上,即当点H与点A重合时,△EGH的高最大;对于△BDH,点H在以BD为直径的圆上,即当点H与点A重合时,△BDH的高最大,即可确定出面积的最大值.
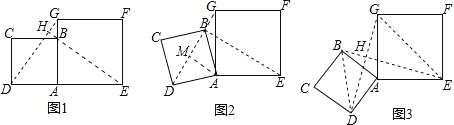
试题解析:(1)∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,∠DAG=∠BAE=90°,AG=AE,
在△ADG和△ABE中,
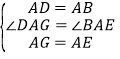 ,
,
∴△ADG≌△ABE(SAS),
∴∠AGD=∠AEB,
如图1所示,延长EB交DG于点H,
在△ADG中,∠AGD+∠ADG=90°,
∴∠AEB+∠ADG=90°,
在△EDH中,∠AEB+∠ADG+∠DHE=180°,
∴∠DHE=90°,
则DG⊥BE;
(2)∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,∠DAB=∠GAE=90°,AG=AE,
∴∠DAB+∠BAG=∠GAE+∠BAG,即∠DAG=∠BAE,
在△ADG和△ABE中,
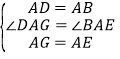
∴△ADG≌△ABE(SAS),
∴DG=BE,
如图2,过点A作AM⊥DG交DG于点M,∠AMD=∠AMG=90°,
∵BD为正方形ABCD的对角线,
∴∠MDA=45°,
在Rt△AMD中,∠MDA=45°,
∴cos45°=![]() ,
,
∵AD=2,
∴DM=AM=![]() ,
,
在Rt△AMG中,根据勾股定理得:GM=![]() ,
,
∵DG=DM+GM=![]() ,
,
∴BE=DG=![]() ;
;
(3)△GHE和△BHD面积之和的最大值为6,理由为:
对于△EGH,点H在以EG为直径的圆上,
∴当点H与点A重合时,△EGH的高最大;
对于△BDH,点H在以BD为直径的圆上,
∴当点H与点A重合时,△BDH的高最大,
则△GHE和△BHD面积之和的最大值为2+4=6.