Question

【题目】如图，∠AOB＝25°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记∠MPQ＝α，∠PQN＝β，当MP＋PQ＋QN最小时，则β﹣α的值为（　　）

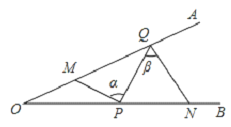
A.50°B.40°C.30°D.25°

Answer 1

【答案】B

【解析】

如图，作M关于OB的对称点M′，N关于OA的对称点N′，连接M′N′交OA于Q，交OB于P，则MP+PQ+QN最小易知∠OPM=∠OPM′=∠NPQ，∠OQP=∠AQN′=∠AQN，根据三角形的外角的性质和平角的定义即可得到结论．

解：如图，作M关于OB的对称点M′，N关于OA的对称点N′，连接M′N′交OA于Q，交OB于P，则MP+PQ+QN最小，

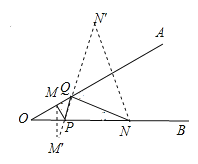
∴∠OPM=∠OPM′=∠NPQ，∠OQP=∠AQN′=∠AQN，

∴∠QPN=（180°-α）=∠AOB+∠MQP=20°+（180°-β），

∴180°-α=40°+（180°-β），

∴β-α=40°，

故选：B．