题目内容
【题目】如图所示，等边△ABC中D点为AB边上一动点，E为直线AC上一点，将△ADE沿着DE折叠，点A落在直线BC上，对应点为F，若AB＝4，BF：FC＝1：3，则线段AE的长度为_____．
【答案】
或14
【解析】
点E在直线AC上，本题分两类讨论，翻折后点F在BC线段上或点F在CB延长线上，根据一线三角的相似关系求出线段长．
解：按两种情况①点F在线段BC上，如图所示，由折叠性质可知
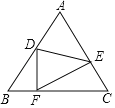
∠A＝∠DFE＝60°
∵∠BFD+∠CFE＝120°，∠BFD+∠BDF＝120°∴∠BDF＝∠CFE∵∠B＝∠C
∴△BDF∽△CFE，∴
∵AB＝4，BF：FC＝1：3
∴BF＝1，CF＝3
设AE＝x，则EF＝AE＝x，CE＝4﹣x
∴
解得BD＝
，DF＝
∵BD+DF＝AD+BD＝4
∴
解得x＝，经检验当x＝时，4﹣x≠0
∴x＝是原方程的解
②当点F在线段CB的延长线上时，如图所示，同理可知
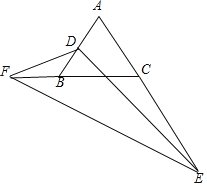
△BDF∽△CFE
∴
∵AB＝4，BF：FC＝1：3，可得BF＝2，CF＝6
设AE＝a，可知AE＝EF＝a，CE＝a﹣4
∴
解得BD＝
，DF＝
∵BD+DF＝BD+AD＝4
∴
解得a＝14
经检验当a＝14时，a﹣4≠0
∴a＝14是原方程的解，综上可得线段AE的长为或14
故答案为或14
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
