题目内容
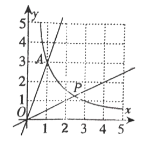
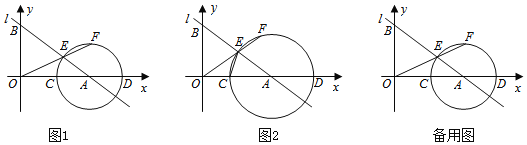
【题目】在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=![]() (k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
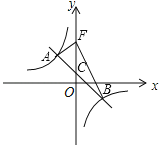
【答案】(1)一次函数的解析式为y=﹣x+1,反比例函数的解析式为y=﹣![]() ;(2)10.
;(2)10.
【解析】
(1)根据待定系数法即可求得;
(2)由一次函数的解析式求得C点的坐标,进而求得CF=4,一次函数的解析式和反比例函数的解析式联立方程求得交点A、B的坐标,然后根据S△ABF=S△ACF+S△BCF求得即可.
(1)把(﹣2,3)分别代入y=﹣x+b,与y=![]() 中,有3=2+b,
中,有3=2+b,![]() =3,
=3,
解得b=1,k=﹣6,
∴一次函数的解析式为y=﹣x+1,反比例函数的解析式为y=﹣![]() ;
;
(2)一次函数的解析式为y=﹣x+1,当x=0时,y=1,
∴C(0,1),
若将点C向上平移4个单位长度得到点F,则CF=4.
∵一次函数y=﹣x+b的图象与反比例函数y=![]() (k≠0)的图象交于A、B两点
(k≠0)的图象交于A、B两点
∴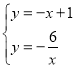 解得
解得![]() ,
,![]() ,
,
∴B(3,﹣2),A(﹣2,3)
∴S△ABF=![]() ×4×(2+3)=10.
×4×(2+3)=10.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目