题目内容
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
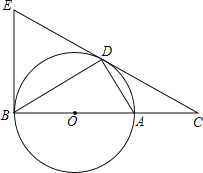
(1)求证:CD2=CACB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
【答案】(1)见解析;(2)见解析;(3)BE的长为5.
【解析】
(1)通过相似三角形(△ADC∽△DBC)的对应边成比例来证得结论.
(2)如图,连接OD.欲证明CD是⊙O的切线,只需证明CD⊥OA即可.
(3)通过相似三角形△EBC∽△ODC的对应边成比例列出关于BE的方程,通过解方程来求线段BE的长度即可.
解:(1)证明:∵∠CDA=∠CBD,∠C=∠C,
∴△ADC∽△DBC,
∴![]() ,即CD2=CACB.
,即CD2=CACB.
(2)证明:如图,连接OD,

∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠1+∠3=90°.
∵OA=OD,
∴∠2=∠3.
∴∠1+∠2=90°.
又∵∠CDA=∠CBD,即∠4=∠1,
∴∠4+∠2=90°,即∠CDO=90°.
∴OD⊥OA.
又∵OA是⊙O的半径,
∴CD是⊙O的切线.
(3)如图,连接OE,
∵EB、CD均为⊙O的切线,
∴ED=EB,OE⊥DB.
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°.
∴∠ABD=∠OEB.
∴∠CDA=∠OEB.
∵tan∠CDA=![]() ,
,
∴![]() .
.
∵Rt△CDO∽Rt△CBE,
∴![]() .
.
∵BC=12,
∴CD=8.
在Rt△CBE中,设BE=x,
∴(x+8)2=x2+122,解得x=5.
∴BE的长为5.

练习册系列答案
相关题目