题目内容
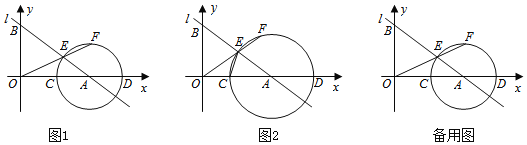
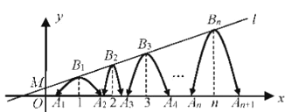
【题目】定义：若抛物线的顶点与
轴的两个交点构成的三角形是直角三角形，则这种抛物线就称为“美丽抛物线”．如图，直线
：
经过点
一组抛物线的顶点
，
，
，…
（
为正整数），依次是直线上的点，这组抛物线与轴正半轴的交点依次是：
，
，
，…
（为正整数）．若
，当
为（ ）时，这组抛物线中存在美丽抛物线．
A.
或
B.或
C.或D.
【答案】B
【解析】
由抛物线的对称性可知，所有构成的直角三角形必是以抛物线顶点为直角顶点的等腰三角形，所以此等腰三角形斜边上的高等于斜边的一半，又0＜d＜1，所以等腰直角三角形斜边的长小于2，所以等腰直角三角形斜边的高一定小于1，即抛物线的顶点纵坐标必定小于1，据此对上一步结论分析可得满足美丽抛物线对应的顶点，再确定抛物线与x轴的交点值与对称轴的距离，从而可求得d的值
解： 直线l：
经过点M（0，
）则b=，
∴直线l：
由抛物线的对称性知：
抛物线的顶点与x轴的两个交点构成的直角三角形必为等腰直角三角形；
∴该等腰三角形的高等于斜边的一半
∵0＜d＜1
∴该等腰直角三角形的斜边长小于2，斜边上的高小于1（即抛物线的顶点纵坐标小于1）∵当x=1时，
＜1；
当x=2时，
＜1；
当x=3时，
＞1；
∴美丽抛物线的顶点只有
①若
为顶点，由
，则
，
②若
为顶点，由
，则
综上所述，d的值为
或
时，存在美丽抛物线．
故选B．
练习册系列答案
相关题目
