题目内容
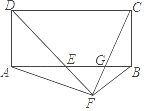
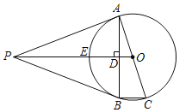
【题目】如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=![]() ,BC=1,求PO的长.
,BC=1,求PO的长.
【答案】(1)见解析;(2)见解析;(3)PO=5
【解析】
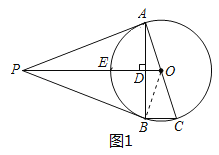
(1)连结OB,如图1,由AC为⊙O的直径可得∠ABC=90°,进而得PO∥BC,然后根据平行线的性质、等腰三角形的性质和等量代换可得∠AOP=∠POB,再根据SAS证明△AOP≌△BOP,可得∠OBP=∠OAP,易知∠OAP=90°,进一步即可证得结论;
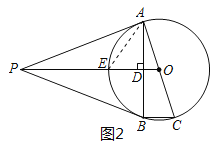
(2)连结AE,如图2,根据切线长定理可得PD平分∠APB,只要根据切线的性质和等角的余角相等证明EA平分∠PAD,然后即可根据三角形内心的概念证得结论;
(3)易得∠PAB=∠C,然后在直角△ABC中根据余弦的定义可求出AC、OA,易证△PAO∽△ABC,进而可根据相似三角形的性质列出比例式,再代入计算即可.
解:(1)证明:连结OB,如图1,
∵AC为⊙O的直径,
∴∠ABC=90°,
∵AB⊥PO,
∴PO∥BC,
∴∠AOP=∠C,∠POB=∠OBC,
∵OB=OC,
∴∠OBC=∠C,
∴∠AOP=∠POB,
在△AOP和△BOP中,∵OA=OB,∠AOP=∠POB,PO=PO,
∴△AOP≌△BOP(SAS),
∴∠OBP=∠OAP,
∵PA为⊙O的切线,
∴∠OAP=90°,
∴∠OBP=90°,
∴PB是⊙O的切线;
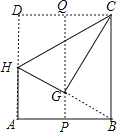
(2)证明:连结AE,如图2,
∵PA为⊙O的切线,
∴∠PAE+∠OAE=90°,
∵AD⊥ED,
∴∠EAD+∠AED=90°,
∵OE=OA,
∴∠OAE=∠AED,
∴∠PAE=∠DAE,
即EA平分∠PAD,
∵PA、PB为⊙O的切线,
∴PD平分∠APB,
∴E为△PAB的内心;
(3)解:∵∠PAB+∠BAC=90°,∠C+∠BAC=90°,
∴∠PAB=∠C,
∴cos∠C=cos∠PAB=![]() ,
,
在Rt△ABC中,cos∠C=![]() =
=![]() ,
,
∴AC=![]() ,AO=
,AO=![]() ,
,
∵∠PAO=∠ABC=90°,∠POA=∠ACB,
∴△PAO∽△ABC,
∴![]() ,即
,即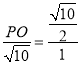 ,
,
解得:PO=5.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案【题目】甲、乙两校各选派10名学生参加“美丽泰州乡土风情知识”大赛预赛.各参赛选手的成绩如下:
甲校:93,98,89,93, 95,96, 93,96,98, 99;
乙校:93,94,88,91,92,93,100, 98,98,93.
通过整理,得到数据分析表如下:
学校 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
甲校 | 99 | a | 95.5 | 93 | 8.4 |
乙校 | 100 | 94 | b | 93 | c |
(1)填空:a = ,b = ;
(2)求出表中c的值,你认为哪所学校代表队成绩好?请写出两条你认为该队成绩好的理由.