题目内容
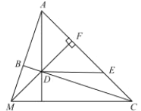
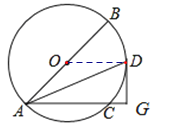
【题目】如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点G.

求证:(1)DG⊥AG;
(2)AG+CG=AB.
【答案】见解析
【解析】
(1)连接OD,根据等腰三角形的性质结合角平分线的性质可得出∠CAD=∠ODA,利用“内错角相等,两直线平行”可得出AE∥OD,结合切线的性质即可证出DG⊥AG;
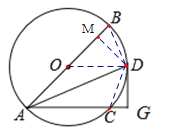
(2)过点D作DM⊥AB于点M,连接CD、DB,根据角平分线的性质可得出DG=DM,
结合AD=AD、∠AGD=∠AMD=90°即可证出△DAG≌△DAM(SAS),根据全等三角形的性质可得出AG=AM,由∠GAD=∠MAD可得出![]() =
= ![]() ,进而可得出CD=BD,结合DG=DM可证出Rt△DGC≌Rt△DMB(HL),根据全等三角形的性质可得出CG=BM,结合AB=AM+BM即可证出AG+CG=AB.
,进而可得出CD=BD,结合DG=DM可证出Rt△DGC≌Rt△DMB(HL),根据全等三角形的性质可得出CG=BM,结合AB=AM+BM即可证出AG+CG=AB.
(1)连接OD,
OA=OD,
∠OAD=∠ODA,
DA平分∠BAC,
则∠OAD=∠CAD,
![]() ∠CAD=∠ODA,
∠CAD=∠ODA,
![]() AE∥OD,
AE∥OD,
DG是⊙O的切线,则![]()
![]() DG⊥AG;
DG⊥AG;
(2)过点D作DM⊥AB于点M,连接CD、DB,
DA平分∠BAC,
DG=DM,
结合AD=AD、∠AGD=∠AMD=90°,
△DAG≌△DAM(SAS),
AE=AM,
由∠GAD=∠MAD,
![]() =
= ![]() ,
,
![]() CD=BD,结合DG=DM可证出Rt△DGC≌Rt△DMB(HL),
CD=BD,结合DG=DM可证出Rt△DGC≌Rt△DMB(HL),
CG=BM,
![]() AB=AM+BM,
AB=AM+BM,
![]() AG+CG=AB.
AG+CG=AB.

【题目】八(2)班分成甲、乙两组进行一分钟投篮测试,并规定得6分及以上为合格,得9分及以上为优秀,现两组学生的一次测试成绩统计如下表:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组人数(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组人数(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上表数据,把下面的统计表补充完整,并写出求甲组平均分的过程;
统计量 | 平均分 | 方差 | 众数 | 中位数 | 合格率 | 优秀率 |
甲组 |
| 2.56 |
| 6 | 80.0% | 26.7% |
乙组 | 6.8 | 1.76 | 7 |
| 86.7% | 13.3% |
(2)如果从投篮的稳定性角度进行评价,你认为哪组成绩更好?并说明理由;
(3)小聪认为甲组成绩好于乙组,请你说出支持小聪观点的理由;