题目内容
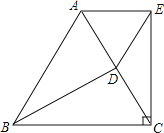
【题目】如图，将矩形纸片ABCD沿其对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E，若AB=8，AD=3，则图中阴影部分的周长为( )
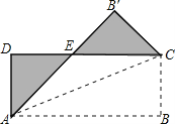
A.16B.19C.22D.25
【答案】C
【解析】
首先由四边形ABCD为矩形及折叠的特性，得到B′C=BC=AD，∠B′=∠B=∠D=90°，∠B′EC=∠DEA，得到△AED≌△CEB′，得出EA=EC，再由阴影部分的周长为AD+DE+EA+EB′+B′C+EC，即矩形的周长解答即可．
解：∵四边形ABCD为矩形，
∴B′C=BC=AD，∠B′=∠B=∠D=90°
∵∠B′EC=∠DEA，
在△AED和△CEB′中，
，
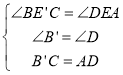∴△AED≌△CEB′(AAS)；
∴EA=EC，
∴阴影部分的周长为AD+DE+EA+EB′+B′C+EC，
=AD+DE+EC+EA+EB′+B′C，
=AD+DC+AB′+B′C，
=3+8+8+3，
=22，
故选：C．
【题目】有两个可以自由转动的质地均匀转盘
、
都被分成了
个全等的扇形，在每一扇形内均标有不同的自然数，如图所示．转动转盘、，两个转盘停止后观察两个指针所指扇形内的数字（若指针停在扇形的边线上，当作指向下方的扇形）．
(1)小明同学转动转盘，小华同学转动转盘，他们都转了
次，结果如下：
指针停靠的扇形内的数字 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
求出表中
的值．
计算盘中“指针停靠的扇形内的数字为
”的频率；
(2)小明转动盘一次，指针停靠的扇形内的数字作为十位数字，小华转动盘一次，指针停靠的扇形内的数字作为个位数字，用列表或画树状图的方法求出“所得的两位数为
的倍数”（记为事件）的概率．
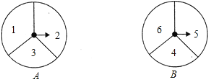
【题目】为了了解江城中学学生的身高情况，随机对该校男生、女生的身高进行抽样调查．已知抽取的样本中，男生、女生的人数相同，根据所得数据绘制成如图所示的统计图表．
组别 | 身高(cm) |
A | x<150 |
B | 150≤x＜155 |
C | 155≤x＜160 |
D | 160≤x＜165 |
E | x≥165 |
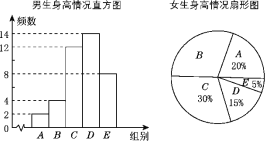
根据图表中提供的信息，回答下列问题：
(1)在样本中，男生身高的中位数落在________组(填组别序号)，女生身高在B组的人数有________人；
(2)在样本中，身高在150≤x＜155之间的人数共有________人，身高人数最多的在________组(填组别序号)；
(3)已知该校共有男生500人、女生480人，请估计身高在155≤x＜165之间的学生有多少人
