题目内容
【题目】在平行四边形ABCD中，在平行四边形内作以线段AD为边的等边△ADM，连结AM．
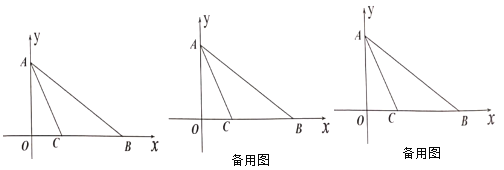
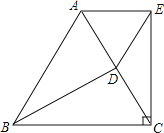
（1）如图1，若点M在对角线BD上，且∠ABC=105°，AB=
，求AM的长；
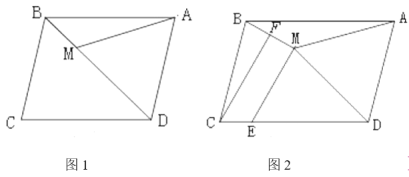
（2）如图2，点E为CD边上一点，连接ME，点F是BM的中点，
，若CE＋ME=DE．求证：BM⊥ME．
【答案】（1）2
（2）见解析
【解析】
（1）过点A作AH⊥BD于H,根据∠ABC=105°和等边三角形、平行四边形的性质得到△ABH为等腰直角三角形，求出AH，再得到AD的长，即可求出AM的长；
（2）在ED上取点G，使得CG＝BM，连接EB，EG．证明△MEC≌△MGD（SAS），△EMG是等边三角形，再得到CF∥ME即可解决问题．
（1）过点A作AH⊥BD于H,
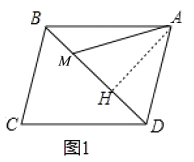
∵△ADM等边三角形，
∴∠ADM=60°，∠DAH=30°
∵四边形ABCD是平行四边形，
∴∠CBD=∠ADM=60°
∵∠ABC=105°，
∴∠ABD=∠ABC -∠CBD=45°
∴△ABH为等腰直角三角形
在Rt△ABH中，AH2＋BH2＝AB2，即2AH2＝18，
∴AH=3，
在Rt△ADH中，∠DAH=30°，
∴AD＝2DH，DH2＋AH2＝AD2，即（
）2＋32＝AD2，
∴AD＝2，
∴AM＝AD＝2；
（2）如图，在ED上取点G，使得DG＝CE，连接CM，MG．
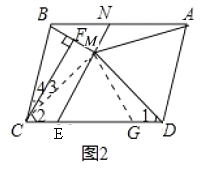
∵F是BM的中点，CF⊥BM，
∴BC＝CM，
∴△BCM是等腰三角形，
∵CF⊥BM，
∴∠3＝∠4，
∵四边形ABCD是平行四边形，
∴BC＝AD，BC∥AD，
∵△ADM是等边三角形，
∴DM＝AD，∠ADM＝60
，
∵BC＝CM，BC＝AD，
∴CM＝DM，
∴∠1＝∠2，
∵CE＝DG
∴△MEC≌△MGD（SAS），
∴EM＝MG，
∵CE＋ME=DE，CG=DE
故CE＋ME=CG= CE＋EG
∴ME= EG
∴EM＝MG= EG
∴△EMG是等边三角形
∴∠MEG＝60
∵BC∥AD，
∴∠BCD＋∠ADC＝180，即∠ADM＋∠1＋∠2＋∠3＋∠4＝180，
∵∠1＝∠2，∠3＝∠4，∠ADM＝60，
∴∠2＋∠3＝60°，即∠FCG＝60，
∴∠MEG＝∠FCG＝60，
∴CF∥EM，
∵CF⊥BM
∴BM⊥ME．
